
Inferenzstatistikverlauf, Merkmale, wofür es ist, Beispiele

Das Inferenzstatistik oder deduktive Statistik ist eine Statistik, die die Merkmale einer Population anhand einer Reihe von Analysetechniken aus den daraus entnommenen Proben ableitet. Mit den erhaltenen Informationen werden Modelle entwickelt, die dann Vorhersagen über das Verhalten dieser Population ermöglichen..
Aus diesem Grund ist die Inferenzstatistik zur Wissenschaft Nummer eins geworden, wenn es darum geht, die Unterstützung und Instrumente anzubieten, die unzählige Disziplinen benötigen, um Entscheidungen zu treffen..

Physik, Chemie, Biologie, Ingenieurwissenschaften und Sozialwissenschaften profitieren kontinuierlich von diesen Werkzeugen, wenn sie ihre Modelle erstellen und Experimente entwerfen und durchführen..
Artikelverzeichnis
- 1 Kurze Geschichte der Inferenzstatistik
- 1.1 Römisches Reich
- 1.2 Mittelalter
- 1.3 Moderne
- 1.4 Zeitgenössisches Zeitalter
- 2 Funktionen
- 3 Wofür ist beschreibende Statistik? Anwendungen
- 3.1 Soziologie und demografische Studien
- 3.2 Engineering
- 3.3 Wirtschaft und Betriebswirtschaft
- 4 Beispiele für Inferenzstatistiken
- 4.1 Beispiel 1
- 4.2 Beispiel 2
- 5 Grundlegende Konzepte in der Inferenzstatistik
- 5.1 Ereignis
- 5.2 Probenraum
- 5.3 Bevölkerung und Stichprobe
- 5.4 Probenahme
- 5.5 Statistische Variablen
- 5.6 Wahrscheinlichkeitsverteilungen
- 5.7 Parameter und Statistiken
- 5.8 Statistische Hypothese
- 5.9 Hypothesentests
- 6 Themen von Interesse
- 7 Referenzen
Kurze Geschichte der Inferenzstatistik
Statistiken entstanden in der Antike aufgrund des Bedürfnisses der Menschen, Dinge zu organisieren und Ressourcen zu optimieren. Vor der Erfindung des Schreibens wurden anhand von in Stein gemeißelten Symbolen Aufzeichnungen über die Anzahl der Personen und das verfügbare Vieh geführt..
Später hinterließen die chinesischen, babylonischen und ägyptischen Herrscher Daten über die Menge der Ernten und die Anzahl der Einwohner, die auf Tontafeln, Säulen und Denkmälern eingraviert waren..
Römisches Reich
Als Rom seine Herrschaft im Mittelmeerraum ausübte, führten die Behörden häufig alle fünf Jahre Volkszählungen durch. Tatsächlich kommt das Wort "Statistik" vom italienischen Wort statista, was bedeutet es auszudrücken.
Zur gleichen Zeit führten in Amerika auch die großen präkolumbianischen Reiche ähnliche Aufzeichnungen.
Mittelalter
Während des Mittelalters registrierten die Regierungen Europas sowie die Kirche das Eigentum an Land. Dann taten sie dasselbe mit Geburten, Taufen, Ehen und Todesfällen.
Modernes Alter
Der englische Statistiker John Graunt (1620-1674) war der erste, der anhand solcher Listen Vorhersagen machte, wie viele Menschen an bestimmten Krankheiten sterben könnten und wie hoch der geschätzte Anteil männlicher und weiblicher Geburten ist. Aus diesem Grund gilt er als Vater der Demografie..
Zeitgenössisches Zeitalter
Später, mit dem Aufkommen der Wahrscheinlichkeitstheorie, war die Statistik keine bloße Sammlung von Organisationstechniken mehr und erreichte als prädiktive Wissenschaft einen unerwarteten Umfang..
Auf diese Weise könnten die Experten beginnen, Modelle für das Verhalten von Bevölkerungsgruppen zu entwickeln und daraus abzuleiten, was mit Menschen, Objekten und sogar Ideen geschehen könnte.
Eigenschaften

Nachfolgend haben wir die wichtigsten Merkmale dieses Statistikzweigs:
- Inferenzstatistik untersucht eine Population, die eine repräsentative Stichprobe daraus entnimmt.
- Die Auswahl der Probe erfolgt nach verschiedenen Verfahren, wobei diejenigen am besten geeignet sind, die die Komponenten nach dem Zufallsprinzip auswählen. Somit hat jedes Element der Bevölkerung die gleiche Wahrscheinlichkeit, ausgewählt zu werden, und somit werden unerwünschte Verzerrungen vermieden..
- Zur Organisation der gesammelten Informationen werden beschreibende Statistiken verwendet.
- An der Stichprobe werden statistische Variablen berechnet, mit denen die Eigenschaften der Population geschätzt werden..
- Inferenz- oder deduktive Statistiken verwenden die Wahrscheinlichkeitstheorie, um zufällige Ereignisse zu untersuchen, dh solche, die zufällig auftreten. Jedem Ereignis ist eine bestimmte Eintrittswahrscheinlichkeit zugeordnet.
- Es konstruiert Hypothesen - Annahmen - über die Parameter der Population und kontrastiert sie, um herauszufinden, ob sie korrekt sind oder nicht, und berechnet auch das Konfidenzniveau der Antwort, dh es bietet eine Fehlerquote. Die erste Prozedur wird aufgerufen Hypothesentest, während die Fehlerquote die ist Konfidenzintervall.
Wofür ist beschreibende Statistik? Anwendungen

Das Studium einer Gesamtbevölkerung kann eine Menge Geld, Zeit und Mühe erfordern. Es ist vorzuziehen, repräsentative Stichproben zu nehmen, die viel einfacher zu verwalten sind, Daten von ihnen zu sammeln und Hypothesen oder Annahmen über das Stichprobenverhalten zu erstellen.
Sobald die Hypothesen aufgestellt und ihre Gültigkeit geprüft sind, werden die Ergebnisse auf die Bevölkerung ausgedehnt und zur Entscheidungsfindung verwendet..
Sie helfen auch dabei, Modelle dieser Bevölkerung zu erstellen und Prognosen für die Zukunft zu erstellen. Aus diesem Grund ist die Inferenzstatistik eine sehr nützliche Wissenschaft für:
Soziologie und demografische Studien
Dies sind ideale Anwendungsbereiche, da statistische Techniken mit der Idee angewendet werden, verschiedene Modelle menschlichen Verhaltens zu etablieren. Etwas, das a priori ziemlich kompliziert ist, da zahlreiche Variablen eingreifen.
In der Politik wird es zur Wahlzeit häufig verwendet, um die Wahltendenz der Wähler zu kennen. Auf diese Weise entwerfen die Parteien Strategien.
Ingenieurwesen
Inferenzstatistikmethoden sind im Ingenieurwesen weit verbreitet. Die wichtigsten Anwendungen sind Qualitätskontrolle und Prozessoptimierung, z. B. die Verbesserung der Arbeitszeiten sowie die Verhinderung von Arbeitsunfällen..
Wirtschaft und Betriebswirtschaft
Mit deduktiven Methoden können Sie Prognosen über den Betrieb eines Unternehmens, das erwartete Umsatzniveau sowie Hilfe bei der Entscheidungsfindung erstellen.
Zum Beispiel können ihre Techniken verwendet werden, um abzuschätzen, wie Käufer auf ein neues Produkt reagieren werden, das kurz vor der Markteinführung steht..
Es dient auch dazu zu bewerten, wie sich die Konsumgewohnheiten der Menschen angesichts wichtiger Ereignisse wie der COVID-Epidemie ändern..
Beispiele für Inferenzstatistiken
Beispiel 1
Ein einfaches deduktives Statistikproblem ist das Folgende: Ein Mathematiklehrer ist für 5 Abschnitte der Elementaralgebra an einer Universität verantwortlich und beschließt, die Durchschnittsnoten von zu verwenden nur einer seiner Abschnitte, um den Durchschnitt von zu schätzen alle.

Eine andere Möglichkeit besteht darin, aus jedem Abschnitt eine Probe zu entnehmen, seine Eigenschaften zu untersuchen und die Ergebnisse auf alle Abschnitte auszudehnen..
Beispiel 2
Der Manager eines Damenbekleidungsgeschäfts möchte wissen, wie viel eine bestimmte Bluse während der Sommersaison verkaufen wird. Dazu analysiert es den Verkauf des Kleidungsstücks in den ersten zwei Wochen der Saison und bestimmt so den Trend..
Grundbegriffe der Inferenzstatistik
Es gibt mehrere Schlüsselkonzepte, einschließlich solcher aus der Wahrscheinlichkeitstheorie, über die Sie sich klar sein müssen, um den vollen Umfang dieser Techniken zu verstehen. Einige haben wir als Grundgesamtheit und Stichprobe bereits im gesamten Text erwähnt.
Veranstaltung
Ein Ereignis oder Ereignis ist etwas, das passiert und das mehrere Ergebnisse haben kann. Ein Beispiel für ein Ereignis könnte das Werfen einer Münze sein, und es gibt zwei mögliche Ergebnisse: Kopf oder Zahl.
Probenraum
Es ist die Menge aller möglichen Ergebnisse eines Ereignisses.
Bevölkerung und Stichprobe
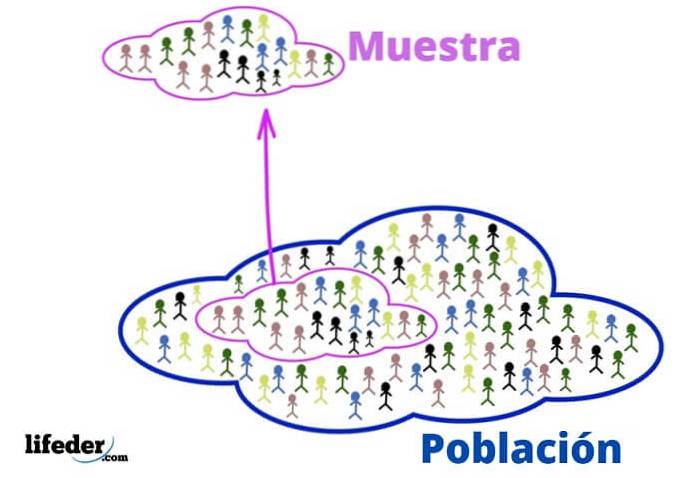
Die Bevölkerung ist das Universum, das Sie studieren möchten. Es geht nicht unbedingt um Menschen oder Lebewesen, da die Bevölkerung in der Statistik aus Objekten oder Ideen bestehen kann.
Die Stichprobe ist ihrerseits eine Teilmenge der Bevölkerung, die sorgfältig daraus extrahiert wurde, weil sie repräsentativ ist..
Probenahme
Dies ist der Satz von Techniken, mit denen eine Stichprobe aus einer bestimmten Population ausgewählt wird. Die Stichprobe kann zufällig sein, wenn probabilistische Methoden zur Auswahl der Stichprobe verwendet werden, oder nicht probabilistisch, wenn der Analytiker nach seiner Erfahrung seine eigenen Auswahlkriterien hat..
Statistische Variablen
Satz von Werten, die die Merkmale der Bevölkerung haben können. Sie werden auf verschiedene Arten klassifiziert, zum Beispiel können sie diskret oder kontinuierlich sein. Unter Berücksichtigung ihrer Natur können sie auch qualitativ oder quantitativ sein..
Wahrscheinlichkeitsverteilungen
Wahrscheinlichkeitsfunktionen, die das Verhalten einer Vielzahl von in der Natur beobachteten Systemen und Situationen beschreiben. Am bekanntesten sind die Gaußsche oder Gaußsche Glockenverteilung und die Binomialverteilung.
Parameter und Statistiken
Die Schätzungstheorie stellt fest, dass es eine Beziehung zwischen den Werten der Bevölkerung und denen der Stichprobe aus dieser Bevölkerung gibt. Das Parameter sind die Merkmale der Bevölkerung, die wir nicht kennen, aber schätzen wollen: zum Beispiel den Mittelwert und die Standardabweichung.
Für ihren Teil, Statistiken sind die Eigenschaften der Probe, zum Beispiel ihr Mittelwert und ihre Standardabweichung.
Nehmen wir zum Beispiel an, die Bevölkerung besteht aus allen jungen Menschen zwischen 17 und 30 Jahren in einer Gemeinde, und wir möchten den Anteil derjenigen kennen, die derzeit eine Hochschulausbildung absolvieren. Dies wäre der zu bestimmende Populationsparameter.
Um dies abzuschätzen, wird eine Zufallsstichprobe von 50 jungen Menschen ausgewählt und deren Anteil an einer Universität oder Hochschule berechnet. Dieser Anteil ist die Statistik.
Wenn nach der Studie festgestellt wird, dass 63% der 50 jungen Menschen eine Hochschulausbildung absolvieren, ist dies die Bevölkerungsschätzung, die aus der Stichprobe abgeleitet wurde.
Dies ist nur ein Beispiel dafür, was Inferenzstatistiken leisten können. Es ist als Schätzung bekannt, aber es gibt auch Techniken zur Vorhersage statistischer Variablen sowie zum Treffen von Entscheidungen.
Statistische Hypothese
Es ist eine Vermutung, die in Bezug auf den Wert des Mittelwerts und die Standardabweichung einiger Merkmale der Bevölkerung gemacht wird. Sofern die Population nicht vollständig untersucht wird, handelt es sich um unbekannte Werte.
Hypothesentest
Sind die getroffenen Annahmen zu den Populationsparametern gültig? Um dies herauszufinden, wird überprüft, ob die Ergebnisse der Stichprobe diese unterstützen oder nicht. Daher müssen Hypothesentests entworfen werden.
Dies sind die allgemeinen Schritte, um einen auszuführen:
Schritt 1
Identifizieren Sie die Art der Verteilung, der die Bevölkerung voraussichtlich folgen wird.
Schritt 2
Geben Sie zwei Hypothesen an, die als H bezeichnet werdenoder und H.1. Der erste ist der Nullhypothese in dem wir annehmen, dass der Parameter einen bestimmten Wert hat. Der zweite ist die alternative Hypothese die einen anderen Wert als die Nullhypothese annimmt. Wenn dies abgelehnt wird, wird die alternative Hypothese akzeptiert.
Schritt 3
Legen Sie einen akzeptablen Spielraum für die Differenz zwischen dem Parameter und der Statistik fest. Diese werden sich selten als identisch herausstellen, obwohl erwartet wird, dass sie sehr nahe beieinander liegen..
Schritt 4
Schlagen Sie ein Kriterium vor, um die Nullhypothese zu akzeptieren oder abzulehnen. Hierzu wird eine Teststatistik verwendet, die der Mittelwert sein kann. Liegt der Mittelwert innerhalb bestimmter Grenzen, wird die Nullhypothese akzeptiert, andernfalls wird sie verworfen.
Schritt 5
Als letzter Schritt wird entschieden, ob die Nullhypothese akzeptiert wird oder nicht..
Themen von Interesse
Zweige der Statistik.
Statistische Variablen.
Bevölkerung und Stichprobe.
Beschreibende Statistik.
Verweise
- Berenson, M. 1985. Statistik für Management und Wirtschaft, Konzepte und Anwendungen. Editorial Interamericana.
- Canavos, G. 1988. Wahrscheinlichkeit und Statistik: Anwendungen und Methoden. Mcgraw Hügel.
- Devore, J. 2012. Wahrscheinlichkeit und Statistik für Ingenieurwesen und Wissenschaft. 8 .. Auflage. Lernen einbinden.
- Geschichte der Statistik. Wiederhergestellt von: eumed.net.
- Ibañez, P. 2010. Mathematik II. Kompetenzansatz. Lernen einbinden.
- Levin, R. 1981. Statistik für Administratoren. Prentice Halle.
- Walpole, R. 2007. Wahrscheinlichkeit und Statistik für Ingenieurwissenschaften und Naturwissenschaften. Pearson.


Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.