
Beschreibende und inferentielle Statistiken

Das Beschreibende Statistik Es ist der Satz statistischer Methoden, die eine Gruppe von Daten beschreiben und / oder charakterisieren. Das Inferenzstatistik versucht, Schlussfolgerungen über allgemeine Situationen abzuleiten und zu ziehen, die über den erhaltenen Datensatz hinausgehen.
Statistik ist eine Disziplin, die für die Verarbeitung und Organisation von Daten verantwortlich ist. Die Daten sind alle Maße oder Werte, die durch Experimente, Umfragen, Volkszählungen oder andere Mittel ermittelt werden können. Die Datenanalyse beginnt normalerweise mit der Anwendung deskriptiver Statistikmethoden und wird dann mit inferentiellen Statistikmethoden fortgesetzt..
| Beschreibende Statistik | Inferenzstatistik | |
|---|---|---|
| Definition | Methoden zur Zusammenfassung der Schlüsselmerkmale bekannter Daten. | Methoden, bei denen Beispieldaten verwendet werden, um Verallgemeinerungen oder Rückschlüsse auf eine Population zu ziehen. |
| Tore | Charakterisieren Sie eine Datengruppe Untersuchen Sie Trends oder Verteilungen | Untersuchen Sie die Unterschiede zwischen den Gruppen. Überprüfen Sie, ob Variablen zugeordnet sind. Vergleichen Sie Durchschnittswerte zwischen Gruppen. Vorhersage einer Variablen von einer anderen. |
| Analysemethoden | Maße der zentralen Tendenz:
Variabilitätsmaße:
|
|
| Anwendungsbereiche | Natur- und Sozialwissenschaften | Sozial- und Naturwissenschaften |
| Beispiele |
|
|
Was ist beschreibende Statistik??
Das Beschreibende Statistik Es ist der Teil der Statistik, der die Daten so anordnet, dass sie analysiert und interpretiert werden können. Beschreibende statistische Methoden ermöglichen es uns:
- Bestimmen Sie die zentrale Tendenz einer Variablen: Mittelwert oder arithmetischer Mittelwert, Median oder Modus.
- Bestimmen Sie die Variabilität einer Variablen: Standardabweichung, Varianz, Bereiche.
- Bestimmen Sie, was die Verteilung einer Variablen: Frequenzhistogramm, Normalverteilung.
Beschreibende Statistikbeispiele
Wenn Sie eine Gruppe von Personen charakterisieren möchten, verwenden Sie beschreibende Statistiken. Zum Beispiel haben wir die folgenden Körpertemperaturdaten für eine Gruppe von Männern und Frauen:
| Männer | Frauen |
|---|---|
| 36.1 | 36.2 |
| 35.9 | 37.2 |
| 36.0 | 37.3 |
| 36.4 | 37.1 |
| 36.3 | 37.0 |
| 36.7 | 37.2 |
| 36.9 | 36.9 |
| 36.8 | 36.8 |
| 37.2 | 36.4 |
| 37.0 | 37.0 |
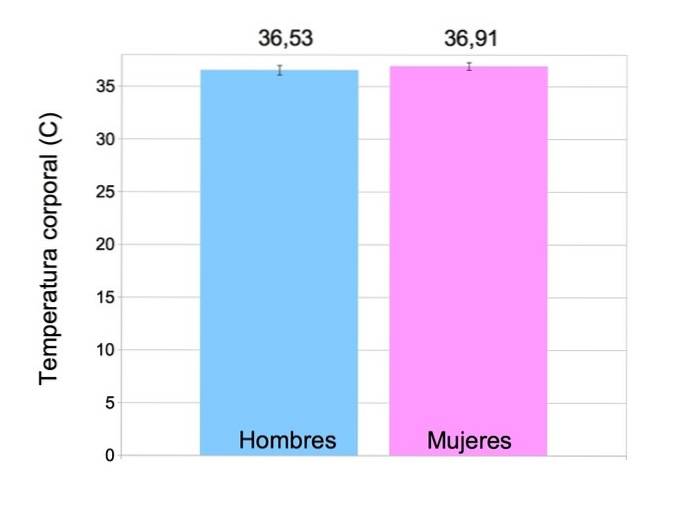
Während sie präsentiert werden, können wir keine Schlussfolgerung ziehen, aber wenn wir deskriptive statistische Techniken anwenden, können wir dann sagen:
- Männer in dieser Gruppe haben eine Durchschnittstemperatur von 36,53 ° C mit einer Standardabweichung von 0,45;
- Frauen in dieser Gruppe haben eine Durchschnittstemperatur von 36,91 ºC mit einer Standardabweichung von 0,36.
Was ist Inferenzstatistik??
Das Inferenzstatistik oder statistische Inferenz ist der Teil der Statistik, der versucht, Merkmale oder erwartete Ergebnisse einer Population vorherzusagen oder abzuleiten, basierend auf den Daten, die aus einer Stichprobe dieser Population erhalten wurden. Unter den Techniken, die in der Inferenzstatistik angewendet werden, sind:
- Der t-Test: wird verwendet, um das arithmetische Mittel zweier Gruppen zu vergleichen, indem bestimmt wird, ob die Unterschiede zwischen den Gruppen zufällig oder systematisch auftreten, was auf einen tatsächlichen Unterschied hinweist.
- Varianzanalyse oder ANOVA: Wird angewendet, um zwei oder mehr Gruppen von Variablen zu vergleichen.
- Die Korrelationsanalyse: zeigt an, ob sich die Werte zwischen zwei Variablen systematisch ändern. Um diese Bestimmungen vorzunehmen, wird der Korrelationskoeffizient verwendet r und der Wert von p oder Konfidenzintervall CI.
- Regressionsanalyse: sagt einen Wert von einem anderen voraus.
Beispiele für Inferenzstatistiken
Wenn wir feststellen möchten, ob ein Verhalten oder ein biologischer Zustand mit einer Krankheit verbunden ist, verwenden wir statistische Inferenzmethoden. Beispielsweise wurden in einer in Deutschland durchgeführten Studie fast sieben Jahre lang 3109 Personen auf unterschiedliche Gesundheitsparameter untersucht. Die Ergebnisse zeigten, dass hohe Blutzuckerspiegel (über 126 mg / dl Fasten), Rauchen und körperliche Inaktivität mit der Entwicklung von Demenz verbunden waren.
Wenn ein neues Medikament entdeckt wird und seine Wirksamkeit bei einer bestimmten Krankheit nachgewiesen werden soll, werden Inferenzstatistiken verwendet. In diesem Fall werden die Wirkungen einer mit dem Arzneimittel behandelten Gruppe und einer anderen mit einem Placebo oder einem Kontrollarzneimittel behandelten Gruppe verglichen..
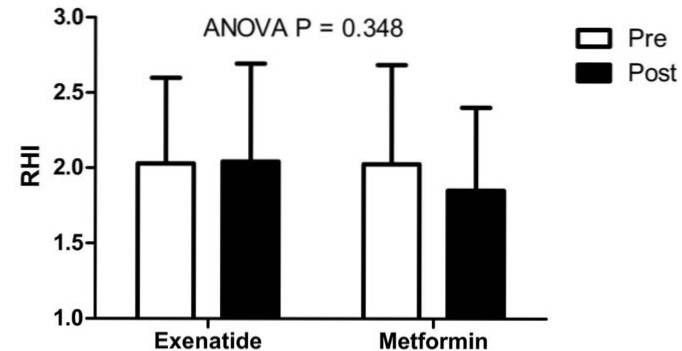
Die Gruppe von Kelly et al. Untersuchte die Endothelfunktion bei 50 übergewichtigen Personen vor (vor) und nach (nach) drei Monaten Behandlung mit zwei Arzneimitteln: Exenatid und Metformin (Kontrolle). Bei der Analyse der Ergebnisse mit der ANOVA-Technik (P = 0,348; Inferenzstatistik) stellten sie fest, dass Exenatid im Vergleich zu Metformin keinen Einfluss auf die Endothelfunktion hatte.
Verweise
Hessler, J. B., Ander, K-H, Brönner, M. et al. (2016) Vorhersage von Demenz bei Patienten in der Grundversorgung mit einer kardiovaskulären Gesundheitsmetrik: eine prospektive bevölkerungsbasierte Studie. BMC Neurol. 16: 116.
Kelly, A. S., Bergenstal, R. M., Gonzalez-Campoy, J. M., Katz, H., Bank, A. J. (2012) Auswirkungen von Exenatide vs Metformin auf die Endothelfunktion bei adipösen Patienten mit Prä-Diabetes: eine randomisierte Studie. Herz-Kreislauf-Diabetologie 11:64.



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.