
Normaler Aufwand, woraus es besteht, wie es berechnet wird, Beispiele
Das normale Anstrengung Auf ein bestimmtes Material angewendet, auch als einachsige Spannung bezeichnet, ist die Beziehung, die zwischen der senkrecht auf eine bestimmte Oberfläche ausgeübten Kraft und der Querschnittsfläche, auf die es wirkt, oder der Last pro Flächeneinheit besteht. Mathematisch gesehen ist die Spannung σ der Quotient, wenn P die Größe der Kraft und A der Bereich ist, in dem sie angewendet wird: σ = P / A..
Die Einheiten der normalen Spannung im internationalen System sind Newton / Meterzwei, bekannt als Pascal und abgekürzt Pa. Dies sind die gleichen Druckeinheiten. Andere Einheiten, die in der Literatur häufig vorkommen, sind Pfund / Zoll.zwei oder psi.

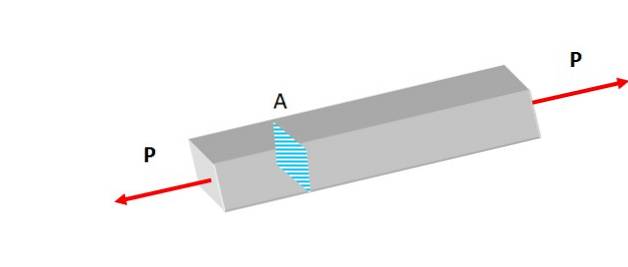
In Abbildung 2 werden zwei Kräfte gleicher Größe senkrecht zur Querschnittsfläche aufgebracht, wodurch eine sehr leichte Traktion auf die Stange ausgeübt wird, die dazu neigt, sie zu verlängern..
Diese Kräfte erzeugen eine normale Spannung, die auch als bezeichnet wird axiale Belastung zentriert, weil seine Wirkungslinie mit der axialen Achse zusammenfällt, auf der der Schwerpunkt liegt.
Bemühungen, ob normal oder auf andere Weise, tauchen ständig in der Natur auf. In der Lithosphäre sind Gesteine der Schwerkraft und der tektonischen Aktivität ausgesetzt und unterliegen Verformungen.
Auf diese Weise entstehen Strukturen wie Falten und Verwerfungen, deren Untersuchung für die Ausbeutung von Mineralien und im Tiefbau für den Bau von Gebäuden und Straßen wichtig ist, um nur einige Beispiele zu nennen..
Artikelverzeichnis
- 1 Wie wird es berechnet??
- 2 Hookesches Gesetz und normaler Stress
- 3 Bedeutung von Stress für die Festigkeit von Materialien und Geologie
- 4 Beispiele
- 4.1 -Übung 1
- 4.2 -Übung 2
- 5 Referenzen
Wie wird es berechnet??
Die zu Beginn angegebene Gleichung σ = P / A ermöglicht die Berechnung der durchschnittlichen Normalspannung über die betreffende Fläche. Der Wert von P ist die Größe der resultierenden Kraft auf die auf den Schwerpunkt ausgeübte Fläche und reicht für viele einfache Situationen aus.
In diesem Fall ist die Kräfteverteilung gleichmäßig, insbesondere an Stellen, an denen die Stange nicht gespannt oder zusammengedrückt wird. Wenn Sie jedoch die Spannung an einem bestimmten Punkt berechnen müssen oder die Kräfte nicht gleichmäßig verteilt sind, sollten Sie die folgende Definition verwenden:
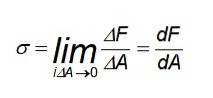
Im Allgemeinen kann der Wert der Spannung an einem bestimmten Punkt vom Durchschnittswert abweichen. Tatsächlich kann der Aufwand je nach zu berücksichtigendem Abschnitt variieren..
Dies ist in der folgenden Abbildung dargestellt, in der die Zugkräfte F versuchen, den Gleichgewichtsstab in den Abschnitten zu trennen mm Y. nn.
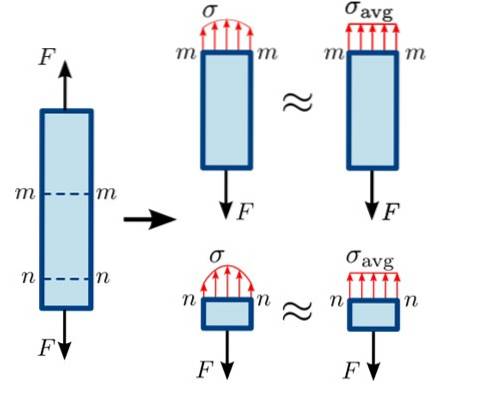
Wie Abschnitt nn sehr nahe an der Stelle, an der die Kraft F nach unten ausgeübt wird, ist die Verteilung der Kräfte auf die Oberfläche nicht vollständig homogen, je geringer die Kraft ist, desto weiter ist sie von diesem Punkt entfernt. Die Verteilung ist im Abschnitt etwas homogener mm.
In jedem Fall tendiert normale Anstrengung immer dazu, die beiden Körperteile, die sich auf beiden Seiten der Ebene befinden, auf die sie wirken, zu dehnen oder zusammenzudrücken. Andererseits neigen andere unterschiedliche Anstrengungen, wie das Scheren, dazu, diese Teile zu verschieben und zu trennen..
Hookesches Gesetz und normaler Stress
Das Hookesche Gesetz besagt, dass innerhalb der Elastizitätsgrenzen die Normalspannung direkt proportional zur Verformung der Stange oder des Objekts ist. In diesem Fall:
Normale Anstrengung ∝ Verformung der Einheit
Als Proportionalitätskonstante Elastizitätsmodul (Y):
Normalspannung (σ) = Elastizitätsmodul (Y) x Einheitsdehnung (ε)
σ = Y. ε
Mit ε = ΔL / L, wobei ΔL die Differenz zwischen der End- und Anfangslänge ist, die L ist.
Der Elastizitätsmodul oder Elastizitätsmodul von Young ist ein Merkmal des Materials, dessen Abmessungen mit denen der Spannung übereinstimmen, da die Einheitsdehnung dimensionslos ist.
Bedeutung von Stress für die Festigkeit von Materialien und Geologie
Es ist sehr wichtig zu bestimmen, wie widerstandsfähig Materialien gegen Beanspruchung sind. Für die beim Bau von Gebäuden sowie bei der Konstruktion von Teilen für verschiedene Geräte verwendeten Strukturen muss sichergestellt sein, dass die gewählten Materialien ihre Funktion angemessen erfüllen.
Aus diesem Grund werden Materialien in Laboratorien anhand von Tests eingehend analysiert, um festzustellen, wie viel Kraft sie aushalten können, bevor sie sich verformen und brechen, wodurch ihre Funktionen verloren gehen. Auf dieser Grundlage wird entschieden, ob sie zur Herstellung eines bestimmten Teils oder eines Teils eines Geräts geeignet sind oder nicht..
Es wird angenommen, dass Leonardo Da Vinci der erste Wissenschaftler war, der die Festigkeit von Materialien systematisch untersuchte. Er hinterließ Hinweise auf Tests, bei denen er den Widerstand von Drähten durch Aufhängen von Steinen mit unterschiedlichem Gewicht bestimmte.
Bei den Bemühungen ist sowohl die Größe der Kraft als auch die Abmessungen der Struktur und die Art und Weise, wie sie angewendet wird, wichtig, um die Grenzen festzulegen, innerhalb derer das Material ein elastisches Verhalten aufweist. Das heißt, es kehrt zu seiner ursprünglichen Form zurück, wenn die Anstrengung aufhört.
Mit den Ergebnissen dieser Tests werden Spannungs-Dehnungs-Kurven für verschiedene Arten von Materialien wie Stahl, Beton, Aluminium und viele mehr erstellt..
Beispiele
Die folgenden Beispiele gehen davon aus, dass die Kräfte gleichmäßig verteilt sind und dass das Material homogen und isotrop ist. Dies bedeutet, dass ihre Eigenschaften in beiden Richtungen gleich sind. Daher gilt es, die Gleichung σ = P / A anzuwenden, um die Kräfte zu finden.
-Übung 1
In 3 ist bekannt, dass die durchschnittliche Normalspannung, die auf den Abschnitt AB wirkt, eine Größe von 48 kPa hat. Finden Sie: a) die Größe der Kraft F, die auf CB wirkt, b) die Spannung auf den Abschnitt BC.
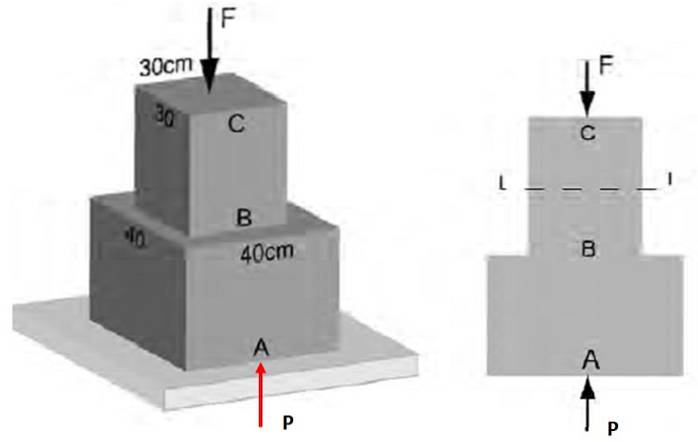
Lösung
Da sich die Struktur nach dem zweiten Newtonschen Gesetz im statischen Gleichgewicht befindet:
P-F = 0
Die normale Belastung des Abschnitts AB hat folgende Größenordnung:
σAB = P / A.AB
Von wo P = σAB . ZUAB = 48000 Pa (40 × 10) -zwei m)zwei = 7680 N.
Daher ist F = 7680 N.
Die normale Spannung auf dem Abschnitt BC ist der Quotient zwischen der Größe von F und der Querschnittsfläche dieser Seite:
σBC = F / A.BC = 7680 N / (30 × 10 -zwei m)zwei = 85,3 kPa.
-Übung 2
Ein Draht mit einer Länge von 150 m und einem Durchmesser von 2,5 mm wird mit einer Kraft von 500 N gespannt.
a) Die Längsspannung σ.
b) Die Einheitsdehnung, wobei bekannt ist, dass die endgültige Länge 150,125 m beträgt.
c) Der Elastizitätsmodul Y. dieses Drahtes.
Lösung
a) σ = F / A = F / π.rzwei
Der Radius des Drahtes beträgt den halben Durchmesser:
r = 1,25 mm = 1,25 × 10-3 m.
Die Querschnittsfläche beträgt π.rzwei, dann ist die Anstrengung:
σ = F / π.rzwei = 500 / (π (1,25 · 10)-3)zwei Pa = 101859,2 Pa
b) ε = ΔL / L = (Endlänge - Anfangslänge) / Anfangslänge
Deshalb:
ε = (150,125 - 150) / 150 = 0,125 / 150 = 0,000833
c) Der Elastizitätsmodul des Drahtes wird unter Kenntnis der zuvor berechneten Werte von ε und σ gelöst:
Y = & sgr; / & egr; = 101859,2 Pa / 0,000833 = 1,22 × 108 Pa = 122 MPa.
Verweise
- Beer, F. 2010. Mechanik der Werkstoffe. 5 .. Auflage. McGraw Hill. 7 - 9.
- Giancoli, D. 2006. Physik: Prinzipien mit Anwendungen. 6tth Ed. Prentice Hall. 238-242.
- Hibbeler, R.C. 2006. Mechanik der Werkstoffe. 6 .. Auflage. Pearson Ausbildung. 22-25
- Valera Negrete, J. 2005. Anmerkungen zur allgemeinen Physik. UNAM. 87-98.
- Wikipedia. Stress (Mechanik). Wiederhergestellt von: wikipedia.org.



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.