
Thermische Gleichgewichtsgleichungen, Anwendungen, Übungen
Das thermische Gleichgewicht zweier Körper, die sich in thermischem Kontakt befinden, ist der Zustand, der nach einer Zeit erreicht wird, die lang genug ist, damit sich die Temperaturen beider Körper ausgleichen.
In der Thermodynamik wird der thermische Kontakt zweier Körper (oder zweier thermodynamischer Systeme) als eine Situation verstanden, in der die Körper mechanischen Kontakt haben oder getrennt sind, aber mit einer Oberfläche in Kontakt stehen, die nur den Wärmeübergang von einem Körper zum anderen ermöglicht (diathermisch) Oberfläche).
-

Abbildung 1. Nach einer Weile erreichen das Eis und das Getränk ihr thermisches Gleichgewicht. Quelle: pixabay
Bei thermischem Kontakt darf keine chemische Reaktion zwischen den in Kontakt stehenden Systemen auftreten. Es sollte nur ein Wärmeaustausch stattfinden.
Alltägliche Situationen, in denen ein Wärmeaustausch stattfindet, treten unter anderem bei Systemen wie dem kalten Getränk und dem Glas, dem heißen Kaffee und dem Teelöffel oder dem Körper und dem Thermometer auf..
Artikelverzeichnis
- 1 Wann befinden sich zwei oder mehr Systeme im thermischen Gleichgewicht??
- 2 Gleichungen des thermischen Gleichgewichts
- 2.1 Gleichgewichtstemperatur
- 2.2 Wärmekontakt mit Phasenwechsel
- 3 Anwendungen
- 3.1 -Übung 1
- 4 Gelöste Übungen
- 4.1 -Übung 2
- 4.2 Übung 3
- 4.3 -Übung 4
- 5 Referenzen
Wenn sich zwei oder mehr Systeme im thermischen Gleichgewicht befinden?
Der zweite Hauptsatz der Thermodynamik besagt, dass Wärme immer vom Körper mit der höchsten Temperatur zum Körper mit der niedrigsten Temperatur gelangt. Die Wärmeübertragung hört auf, sobald sich die Temperaturen angleichen und der Zustand des thermischen Gleichgewichts erreicht ist..
Die praktische Anwendung des thermischen Gleichgewichts ist das Thermometer. Ein Thermometer ist ein Gerät, das seine eigene Temperatur misst. Dank des thermischen Gleichgewichts können wir jedoch die Temperatur anderer Körper wie der einer Person oder eines Tieres ermitteln.
Das Quecksilbersäulenthermometer wird in thermischen Kontakt mit dem Körper gebracht, beispielsweise unter die Zunge, und es wird genügend Zeit gewartet, bis das thermische Gleichgewicht zwischen dem Körper und dem Thermometer erreicht ist und sein Messwert nicht weiter variiert.
Wenn dieser Punkt erreicht ist, entspricht die Temperatur des Thermometers der des Körpers.
Das Nullgesetz der Thermodynamik besagt, dass, wenn sich ein Körper A im thermischen Gleichgewicht mit einem Körper C befindet und sich derselbe Körper C im thermischen Gleichgewicht mit B befindet, A und B sich im thermischen Gleichgewicht befinden, selbst wenn kein thermischer Kontakt zwischen A und B besteht.
Wir schließen daraus, dass zwei oder mehr Systeme bei gleicher Temperatur im thermischen Gleichgewicht sind.
Thermische Gleichgewichtsgleichungen
Wir nehmen einen Körper A mit der Anfangstemperatur Ta in thermischem Kontakt mit einem anderen Körper B mit der Anfangstemperatur Tb an. Wir nehmen auch an, dass Ta> Tb, dann wird nach dem zweiten Gesetz die Wärme von A nach B übertragen.
Nach einer Weile ist das thermische Gleichgewicht erreicht und beide Körper haben die gleiche Endtemperatur Tf. Dies hat einen Zwischenwert bei Ta und Tb, dh Ta> Tf> Tb.
Die von A nach B übertragene Wärmemenge Qa ist Qa = Ma Ca (Tf - Ta), wobei Ma die Masse des Körpers A, Ca die Wärmekapazität pro Masseneinheit von A und (Tf - Ta) die Temperaturdifferenz ist. Wenn Tf kleiner als Ta ist, ist Qa negativ, was anzeigt, dass der Körper A Wärme abgibt.
In ähnlicher Weise haben wir für den Körper B, dass Qb = Mb Cb (Tf - Tb); und wenn Tf größer als Tb ist, ist Qb positiv, was anzeigt, dass Körper B Wärme empfängt. Da Körper A und Körper B in thermischem Kontakt miteinander stehen, jedoch von der Umgebung isoliert sind, muss die Gesamtmenge der ausgetauschten Wärme Null sein: Qa + Qb = 0
Dann ist Ma Ca (Tf - Ta) + Mb Cb (Tf - Tb) = 0
Gleichgewichtstemperatur
Durch Entwickeln dieses Ausdrucks und Auflösen der Temperatur Tf wird die Endtemperatur des thermischen Gleichgewichts erhalten.
-

Abbildung 2. Endgleichgewichtstemperatur. Quelle: selbst gemacht
Tf = (Ma Ca Ta + Mb Cb Tb) / (Ma Ca + Mb Cb).
Betrachten Sie als besonderen Fall den Fall, dass die Körper A und B in Masse und Wärmekapazität identisch sind. In diesem Fall beträgt die Gleichgewichtstemperatur:
Tf = (Ta + Tb) / 2 ↔ wenn Ma = Mb und Ca = Cb.
Wärmekontakt mit Phasenwechsel
In einigen Situationen kommt es vor, dass der Wärmeaustausch, wenn zwei Körper in thermischen Kontakt gebracht werden, die Änderung des Zustands oder der Phase in einem von ihnen verursacht. In diesem Fall muss berücksichtigt werden, dass während des Phasenwechsels keine Temperaturänderung im Körper auftritt, die seinen Zustand verändert.
Wenn die Phasenänderung eines der Körper in thermischem Kontakt auftritt, wird das Konzept der latenten Wärme L angewendet, bei der es sich um die Energie pro Masseneinheit handelt, die für die Zustandsänderung erforderlich ist:
Q = L ∙ M.
Zum Schmelzen von 1 kg Eis bei 0 ° C sind beispielsweise 333,5 kJ / kg erforderlich, und dieser Wert ist die latente Wärme L des Eisschmelzens.
Während des Schmelzens wechselt es von festem zu flüssigem Wasser, aber dieses Wasser behält während des Schmelzprozesses die gleiche Temperatur wie Eis bei..
Anwendungen
Das thermische Gleichgewicht gehört zum täglichen Leben. Lassen Sie uns zum Beispiel diese Situation im Detail untersuchen:
-Übung 1
Eine Person möchte in warmem Wasser bei 25 ° C baden. In einen Eimer 3 Liter kaltes Wasser bei 15 ° C geben und in der Küche Wasser auf 95 ° C erhitzen.
Wie viele Liter heißes Wasser sollten Sie in den Eimer mit kaltem Wasser geben, um die gewünschte Endtemperatur zu erreichen??
Lösung
Angenommen, A ist kaltes Wasser und B ist heißes Wasser:
-
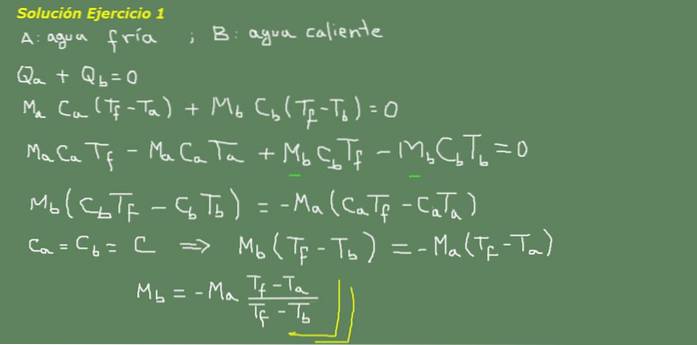
Abbildung 3. Übungslösung 3. Quelle: eigene Ausarbeitung.
Wir schlagen die Gleichung des thermischen Gleichgewichts vor, wie an der Tafel in Abbildung 3 angegeben, und lösen von dort aus die Wassermasse Mb.
Die anfängliche Masse an kaltem Wasser kann erhalten werden, weil die Dichte des Wassers bekannt ist, die 1 kg pro Liter beträgt. Das heißt, wir haben 3 kg kaltes Wasser.
Ma = 3 kg
Dann
Mb = - 3 kg * (25 ° C - 15 ° C) / (25 ° C - 95 ° C) = 0,43 kg
Dann reichen 0,43 Liter heißes Wasser aus, um schließlich 3,43 Liter warmes Wasser bei 25 ° C zu erhalten.
Gelöste Übungen
-Übung 2
Ein Stück Metall mit einer Masse von 150 g und einer Temperatur von 95 ° C wird in einen Behälter mit einem halben Liter Wasser bei einer Temperatur von 18 ° C gegeben. Nach einer Weile ist das thermische Gleichgewicht erreicht und die Temperatur des Wassers und des Metalls beträgt 25 ° C..
Angenommen, der Behälter mit dem Wasser und dem Metallstück ist eine geschlossene Thermoskanne, die keinen Wärmeaustausch mit der Umgebung ermöglicht.
Erhalten Sie die spezifische Wärme des Metalls.
Lösung
Zuerst berechnen wir die vom Wasser aufgenommene Wärme:
Qa = Ma Ca (Tf - Ta)
Qa = 500 g 1cal / (g ° C) (25 ° C - 18 ° C) = 3500 Kalorien.
Das ist die gleiche Wärme, die das Metall abgibt:
Qm = 150 g Cm (25 ° C - 95 ° C) = -3500 Kalorien.
So können wir die Wärmekapazität des Metalls erhalten:
Cm = 3500 cal / (150 g 70 ° C) = ⅓ cal / (g ° C).
Übung 3
Sie haben 250 c.c. Wasser bei 30 ° C. Zu dem Wasser, das sich in einer isolierenden Thermoskanne befindet, werden 25 g Eiswürfel bei 0 ° C gegeben, um es abzukühlen.
Bestimmen Sie die Gleichgewichtstemperatur; Das heißt, die Temperatur, die verbleibt, wenn das gesamte Eis geschmolzen ist und sich das Eiswasser erwärmt hat, um anfänglich der des Wassers im Glas zu entsprechen.
Lösung 3
Diese Übung kann in drei Schritten gelöst werden:
- Das erste ist das Schmelzen von Eis, das Wärme vom ursprünglichen Wasser absorbiert, um zu schmelzen und Wasser zu werden..
- Dann wird der Temperaturabfall im Ausgangswasser berechnet, da es Wärme abgegeben hat (Qced<0) para fundir el hielo.
- Schließlich muss das geschmolzene Wasser (das aus dem Eis kommt) thermisch mit dem ursprünglich vorhandenen Wasser ausgeglichen werden..
-

Abbildung 4. Lösung für Übung 3. Quelle: eigene Ausarbeitung.
Berechnen wir die Wärme, die zum Schmelzen des Eises benötigt wird:
Qf = L · Mh = 333,5 kJ / kg · 0,025 kg = 8,338 kJ
Dann ist die Wärme, die das Wasser zum Schmelzen des Eises gibt, Qced = -Qf
Diese vom Wasser abgegebene Wärme senkt seine Temperatur auf einen Wert T ', den wir wie folgt berechnen können:
T '= T0 - Qf / (Ma · Ca) = 22,02ºC
Wobei Ca die Wärmekapazität von Wasser ist: 4,18 kJ / (kg ° C).
Schließlich gibt die ursprüngliche Wassermasse, die sich jetzt bei 22,02 ° C befindet, Wärme an die Masse des geschmolzenen Wassers aus dem Eis bei 0 ° C ab..
Schließlich wird die Gleichgewichtstemperatur Te nach ausreichender Zeit erreicht:
Te = (Ma · T '+ Mh · 0ºC) / (Ma · Mh) = (0,25 kg · 22,02ºC + 0,025 kg · 0ºC) / (0,25 kg + 0,025 kg).
Endlich die Gleichgewichtstemperatur erhalten:
Te = 20,02 ° C..
-Übung 4
Ein 0,5 kg schweres Stück Blei kommt bei einer Temperatur von 150 ° C aus dem Ofen, die weit unter seinem Schmelzpunkt liegt. Dieses Stück wird in einen Behälter mit 3 Litern Wasser bei einer Raumtemperatur von 20 ° C gegeben. Bestimmen Sie die endgültige Gleichgewichtstemperatur.
Berechnen Sie auch:
- Wärmemenge, die von Blei an Wasser abgegeben wird.
- Wärmemenge, die vom Wasser aufgenommen wird.
Daten:
Spezifische Wärme von Blei: Cp = 0,03 cal / (g ° C); spezifische Wärme von Wasser: Ca = 1 cal / (g ° C).
Lösung
Zuerst bestimmen wir die endgültige Gleichgewichtstemperatur Te:
Te = (Ma Ca Ta + Mp Cp Tp) / (Ma Ca + Mp Cp)
Te = 20,65 ° C.
Dann ist die von Blei freigesetzte Wärmemenge:
Qp = Mp Cp (Te - Tp) = -1,94 · 10³ cal.
Die vom Wasser aufgenommene Wärmemenge beträgt:
Qa = Ma Ca (Te - Ta) = + 1,94 · 10³ cal.
Verweise
- Atkins, P. 1999. Physikalische Chemie. Omega-Ausgaben.
- Bauer, W. 2011. Physik für Ingenieurwissenschaften. Band 1. Mc Graw Hill.
- Giancoli, D. 2006. Physik: Prinzipien mit Anwendungen. 6.… Ed Prentice Hall.
- Hewitt, Paul. 2012. Konzeptionelle Physik. 5 .. Ed. Pearson.
- Resnick, R. (1999). Körperlich. Vol. 1. 3rd Ed. In Spanisch. Compañía Editorial Continental S.A. von C.V..
- Rex, A. 2011. Grundlagen der Physik. Pearson.
- Sears, Zemansky. 2016. Universitätsphysik mit moderner Physik. 14 .. Ed. Band 1.
- Serway, R., Jewett, J. (2008). Physik für Wissenschaft und Technik. Band 1. 7 .. Ed. Lernen einbinden.



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.