Ein erweiterter Körper soll sich in befinden Rotationswaage wenn die Summe der darauf einwirkenden Drehmomente Null ist. Dies bedeutet nicht, dass das Objekt notwendigerweise in Ruhe ist, sondern dass es keine Nettotendenz gibt, seinen Bewegungszustand für ein anderes zu ändern..
Ein Objekt, das sich mit konstanter Geschwindigkeit bewegt, bewegt sich entlang einer geraden Linie, und wir können es im Rotationsgleichgewicht betrachten. Jetzt drehen sich Objekte, weil Kräfte auf sie einwirken, so dass sich eine Drehung ergibt. Die Fähigkeit einer Kraft, eine Rotation zu erzeugen, die als Drehmoment oder bezeichnet wird Torca, hängt nicht nur von der Intensität der Kraft ab, sondern auch davon, wo sie angewendet wird.
Wir erkennen dies sofort, wenn eine geschlossene Tür geöffnet werden soll: In der Nähe der Scharniere wird niemals Kraft ausgeübt, sondern von diesen weg. Deshalb wird der Griff so weit wie möglich auf der gegenüberliegenden Seite der Tür platziert.
Die Drehachse der Tür verläuft durch die Scharniere. Das Bestehen darauf, es sehr nahe an die Scharniere zu drücken, erfordert große Anstrengungen, um die Tür noch ein wenig zu bewegen..
In der Literatur wird das Drehmoment unter verschiedenen Namen gefunden: Drehmoment, Torsion, Kraftmoment und Drehmoment. Sie sind alle synonym.
Wir müssen also die Drehmomente kennen, die auf ein Objekt wirken, um die Rotationsgleichgewichtsbedingung herzustellen.
Artikelverzeichnis
Die Rotationsgleichgewichtsbedingung ist:
Die Summe aller Momente oder Drehmomente, die auf einen Körper wirken, berechnet in Bezug auf eine Achse, muss Null sein.
Das betreffende Objekt muss gedehnt werden, da Partikel per Definition nur ein Translationsgleichgewicht aufweisen.
Es können Kräfte auf den Körper ausgeübt werden und es besteht immer noch ein Rotationsgleichgewicht, solange die Kräfte ihn nicht drehen lassen.
Es kann auch eine Bewegung geben, sogar beschleunigt, aber immer entlang einer geraden Linie, da nicht alle Kräfte das Auftreten von Drehmomenten verursachen. Diese treten auf, wenn die Kräfte nicht alle entlang derselben Wirkungslinie wirken..
Das Drehmoment wird mit dem griechischen Buchstaben bezeichnet τ, auf fettgedruckte Schriftart weil es ein Vektor ist und wir ihn daher von seiner Größe oder seinem Modul unterscheiden, das ein Skalar ist. Es kommt auf die aufgebrachte Kraft an F., Vektor r das ist von der Drehachse O zum Angriffspunkt der Kraft und schließlich vom Winkel zwischen diesen beiden Vektoren gerichtet.
Das Vektorprodukt stellt die geeignete Beziehung zwischen diesen Größen her:
τ = r x F.
Und das ohne Fettdruck bezeichnete Drehmomentmodul lautet:
τ = r⋅F⋅sen θ
Wobei θ der Winkel zwischen ist r Y. F.. Die Drehmomenteinheiten sind im internationalen System einfach Nm.
In der Abbildung befindet sich ein Schraubenschlüssel, mit dem eine Mutter gegen den Uhrzeigersinn (gegen den Uhrzeigersinn) gedreht werden soll. Hierzu wird es mit zwei Kräften getestet F.ZU Y. F.B..
F.ZU ist näher an O und hat einen Vektor rZU oder kürzerer Hebelarm, daher erzeugt er nicht so viel Drehmoment wie die Kraft F.B., das hat die gleiche Größe, hat aber einen Vektor rB. größer.
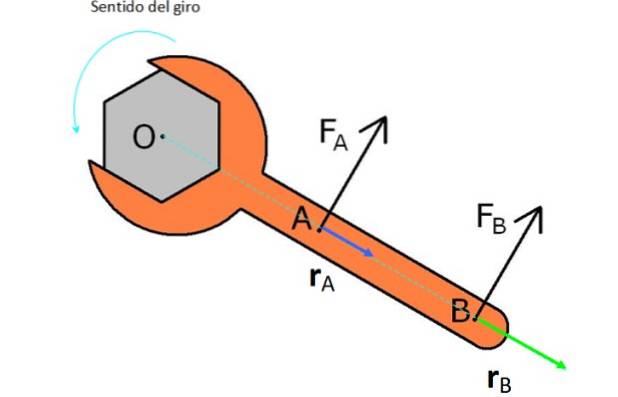
Beachten Sie, dass Sie, wenn Sie die Mutter im Uhrzeigersinn drehen möchten, die Kräfte in die entgegengesetzte Richtung anwenden müssen, wie sie in der Abbildung dargestellt sind.
Da sich das Drehmoment aus dem Kreuzprodukt zwischen den Kraft- und Positionsvektoren ergibt und diese in der Ebene des Schraubenschlüssels liegen, muss das Drehmoment ein Vektor senkrecht zu dieser Ebene sein, dh auf den Leser oder auf die Innenseite des Schlüssels gerichtet Seite.
Konventionell ist das Drehmoment positiv, wenn es sich gegen den Uhrzeigersinn dreht, und negativ, wenn es sich im Uhrzeigersinn dreht..
Die Richtung und der Sinn des resultierenden Drehmoments können leicht durch die unten gezeigte rechte Regel bestimmt werden:
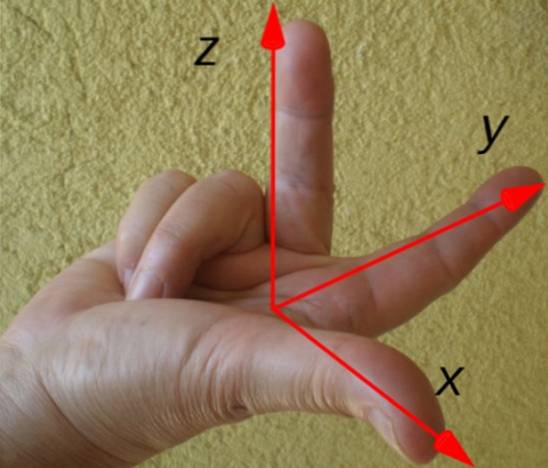
Der Zeigefinger zeigt entsprechend dem Positionsvektor r, Mittelfinger nach Stärke F. und der Daumen zeigt die Richtung und das Gefühl des Drehmoments τ. In diesem Beispiel ist das Drehmoment gemäß der Zeichnung der Koordinatenachsen entlang der x-Achse gerichtet.
Wenn Drehmomente auf einen Körper wirken τ1, τzwei, τ3… τich, das Netto- oder resultierende Drehmoment τn ist die Vektorsumme von allen:
τn = τ1+ τzwei + τ3 +... τich
Mit Summationsnotation bleibt es:
τn = ∑ τich
Die Gleichgewichtsbedingung wird mathematisch wie folgt ausgedrückt:
τn = 0
Ach ja:
∑ τich = 0
Wo das Drehmoment τ, in Bezug auf eine bestimmte Achse O wird berechnet durch:
τ = r x F.
Und wessen Größe ist:
τ = r⋅F⋅sen θ
-Bei Menschen und Tieren ist Gewicht eine Kraft, die Drehmoment, Spin und Sturz verursachen kann.
Menschen halten im Allgemeinen eine Haltung ein, in der sie beim Gehen im Rotationsgleichgewicht bleiben, es sei denn, sie üben sportliche Aktivitäten wie Gymnastik, Skaten oder Sport im Allgemeinen aus..
-Zwei Jungen, die es geschafft haben, horizontal in der zu bleiben Rocker oder auf und ab sind im Rotationsgleichgewicht.
-Wenn die Ausgleichswannen ausbalanciert sind, befindet sich das System im Rotationsgleichgewicht.
-Schilder und Ampeln, die an Straßen und Alleen hängen, befinden sich ebenfalls im Rotationsgleichgewicht. Wenn die Kabel, die sie halten, brechen, geht dieses Gleichgewicht verloren und das Schild hängt oder fällt..
-Hängebrücken wie das Golden Gate in San Francisco und die Brücke in Abbildung 1.
Die in der Abbildung gezeigte Stützstange ist sehr leicht. Die von der Stütze ausgeübte Kraft ist F. und ganz rechts wird Kraft ausgeübt ZU.
Es wird angefordert, die Größen dieser Kräfte unter Berücksichtigung der Tatsache zu berechnen, dass sich das System im Translations- und Rotationsgleichgewicht befindet.
Da sich das System nicht bewegt, wird die Summe der Kräfte aufgehoben. Sie sind alle vertikal und können mit den Größen bearbeitet werden. Die positive Richtung ist nach oben und die negative Richtung ist nach unten, daher:
F - 80 - A = 0
Nun wird die Rotationsgleichgewichtsbedingung angewendet, für die wir eine beliebige Rotationsachse wählen müssen. In diesem Fall wird es ganz rechts gewählt, so dass der Vektor rZU ist null, auf diese Weise ist das Drehmoment von ZU, aber nur die von F. und die Kraft der Linken.
Das Drehmoment von F. ist nach der rechten Regel und dem gezeigten Koordinatensystem:
τF. = rF. x F. = 0,9 F (-k) N.m.
Es ist auf die Innenseite des Bildschirms gerichtet und hat ein negatives Vorzeichen. Während das durch die 80 N Kraft erzeugte Drehmoment ist:
τ = 80 x 1,20 (k) N⋅m = 96 (k) N⋅m
Dieses Drehmoment ist vom Bildschirm weg gerichtet und erhält ein positives Vorzeichen. Wie es ein Rotationsgleichgewicht gibt:
96 - 0,9 · F = 0
Die Größe von F. es ist:
F = (96 / 0,9) N = 106,7 N.
Und da sich das System im Translationsgleichgewicht befindet, hebt sich die Summe der Kräfte auf. Dies ermöglicht es uns, für die Größe von zu lösen ZU::
F - A - 80 N = 0
Deshalb:
A = 106,7 - 80 N = 26,7 N..
Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.