
Translationale Gleichgewichtsbedingungen, Beispiele, Übungen
Es wird behauptet, dass sich ein Objekt in befindet Translationsgleichgewicht wenn die Summe der auf sie einwirkenden Kräfte Null ist. Dies bedeutet nicht, dass es notwendigerweise Ruhe gibt, aber die Bewegung, falls vorhanden, wäre im Fall eines großen Objekts gleichmäßig geradlinig oder ausschließlich rotierend..
Die Bedingungen des mechanischen Gleichgewichts basieren auf den Newtonschen Gesetzen der Mechanik. In der Tat sagt uns das erste Gesetz, dass sich ein Objekt in Ruhe befindet oder mit einer MRU mit gleichmäßiger geradliniger Bewegung bewegt, vorausgesetzt, es wirkt keine Nettokraft auf es.

Die Nettokraft oder resultierende Kraft ist nun einfach die Vektorsumme aller auf das Objekt einwirkenden Kräfte. Nach dem zweiten Newtonschen Gesetz muss diese Summe gleich dem Produkt zwischen Masse und Beschleunigung sein, aber wenn das Objekt nicht beschleunigt wird, verschwindet diese Summe.
Und ohne Beschleunigung gibt es die beiden oben genannten Möglichkeiten: Der Körper ist in Ruhe, dh er bewegt sich nicht, oder wenn dies der Fall ist, muss er sich in der MRU befinden. Im ersten Fall sprechen wir vom statischen transnationalen Gleichgewicht und im zweiten vom dynamischen.
Das translatorische Gleichgewicht ist ein wichtiger Faktor in vielen Aspekten des Ingenieurwesens, beispielsweise im Bauwesen. Die Elemente, aus denen ein Gebäude besteht: Balken, Kabel, Rahmen und mehr, müssen im Gleichgewicht sein, um die Stabilität des Gehäuses zu gewährleisten.
Das Gleichgewicht der Translation wird auch in mobilen Strukturen wie Rolltreppen, Förderbändern und in der Ausübung zahlreicher Sportarten angestrebt..
Artikelverzeichnis
- 1 Bedingung des Translationsgleichgewichts
- 1.1 Freikörperdiagramme
- 2 Beispiele für das Translationsgleichgewicht
- 2.1 Gebäude und Straßen
- 2.2 Bücher und Gegenstände in Regalen
- 2.3 Die Möbel
- 2.4 Ampeln
- 2.5 Öffentliche Beleuchtung
- 3 Übung gelöst
- 3.1 Lösung
- 4 Referenzen
Translationale Gleichgewichtsbedingung
Angenommen, mehrere Kräfte wirken auf einen Körper, den wir als bezeichnen F.1, F.zwei, F.3... . F.n, Verwenden Sie Fettdruck, um die Tatsache hervorzuheben, dass Kräfte Vektoren sind und als solche hinzugefügt werden müssen.
Die Vektorsumme all dieser Kräfte heißt resultierende Kraft oder Nettokraft. Wenn diese Summation den Nullvektor ergibt, ist die Bedingung für das Translationsgleichgewicht erfüllt:
F.1+ F.zwei+ F.3... .+ F.n = 0
Diese Bedingung kann kompakt mit der Summationsnotation geschrieben werden:
∑ F.ich = 0
In Bezug auf die Komponenten der resultierenden Kraft kann die obige Gleichung, die ein Vektor ist, in drei Skalargleichungen zerlegt werden, eine für jede Komponente der resultierenden Kraft:
∑ F.ix = 0; ∑ F.Y. = 0 und ∑ F.z = 0
In der Praxis ist es nicht einfach, die Summe der Kräfte aufzuheben, da Reibung eine Kontaktkraft zwischen Oberflächen ist, die durch keine andere Kraft kaum vollständig aufgehoben wird..
Dies ist der Grund, warum reale Objekte fast nie von äußeren Kräften befreit sind und es folglich schwierig ist, ein Translationsgleichgewicht zu erreichen.
Daher verwenden Ingenieure Mechanismen zur Verringerung der Reibung, wie z. B. Lager und die Verwendung von Schmierölen..
Freikörperdiagramme
Das Freikörperdiagramm ist ein Diagramm, in dem die auf den Körper einwirkenden Kräfte gezeichnet werden. Bei der Suche nach einem translatorischen Gleichgewicht müssen diese Kräfte ausgeglichen werden. Wenn beispielsweise eine nach unten gerichtete vertikale Kraft wie das Gewicht wirkt, muss eine vertikale Kraft nach oben vorhanden sein, die genau die gleiche Größe hat.
Diese Kraft kann von der Hand aufgebracht werden, die das Objekt so stützt, dass es nicht herunterfällt, von einem Seil oder einfach von der Oberfläche eines Tisches.
Wenn eine Kraft tangential zur Oberfläche ist, wie z. B. kinetische oder statische Reibung, muss eine andere Gegenkraft vorhanden sein, damit das Gleichgewicht besteht. Schauen wir uns zum Beispiel das Gewicht an, das an den in der folgenden Abbildung gezeigten Saiten hängt.
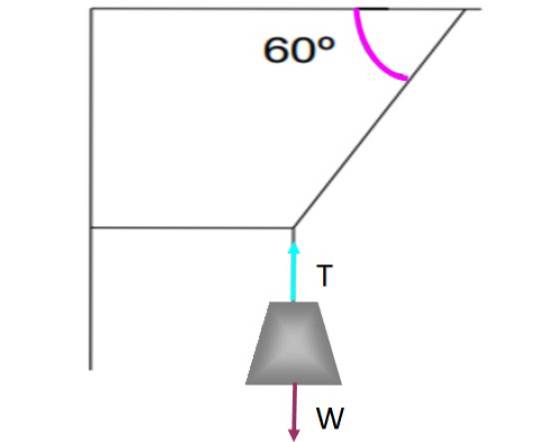
Dank des vertikalen Seils, das es durch Ausüben einer Spannung hält, bleibt das Gewicht im translatorischen Gleichgewicht und ohne sich zu bewegen T. das gleicht das Gewicht aus W.. Jede Kraft wurde auf dem Gewicht durch einen Pfeil dargestellt, jeder von gleicher Größe und mit derselben Richtung, aber entgegengesetzter Richtung..
Die ausgleichende Kraft
Angenommen, eine Reihe von Kräften wirkt auf ein Objekt. Dies nennt man a Kraftsystem Daraus kann das Ergebnis wie oben erläutert ermittelt werden: durch vektorielle Addition jeder der Kräfte des Systems.
Nun, die Kraft, die dieser Resultierenden entgegengesetzt ist, heißt Ausgleichskraft. Wenn die resultierende Kraft ist F.R. und die ausgleichende Kraft ist UND, dann:
UND + F.R. = 0
Deshalb:
UND = - F.R.
Beispiele für das Translationsgleichgewicht
Viele Objekte, die wir täglich innerhalb und außerhalb des Hauses finden, befinden sich im translatorischen Gleichgewicht:
Gebäude und Straßen
Gebäude und Straßen sind so gebaut, dass sie stabil bleiben und nicht umkippen oder einstürzen. In Wolkenkratzern und im Allgemeinen in sehr hohen Gebäuden ist jedoch eine gewisse Flexibilität erforderlich, um der Einwirkung des Windes zu widerstehen..
Bücher und Gegenstände in Regalen
Bücher in einer Bibliothek und Produkte in Verkaufsregalen sind Objekte, die im translatorischen Gleichgewicht bleiben und sich nicht bewegen..
Die Möbel
Die Möbel, der Flachbildfernseher und die Bilder an der Wand sowie die von der Decke hängenden Lampen, um nur einige Objekte zu nennen, sind in translatorischer Balance..
Ampeln
Die Ampeln sind mit Masten und Kabeln befestigt, damit sie nicht herunterfallen. Wir wissen jedoch, dass der Wind sie schwanken lässt.
Öffentliche Beleuchtung
Die Straßenlaternen sind ebenfalls in translatorischer Balance und an den Laternenpfählen befestigt, wie die Straßenlaterne im Hauptbild..
Übung gelöst
Wie groß muss die Kraft sein F.s der Haftreibung, so dass der Kasten in der Figur in der Mitte der schiefen Ebene in einem Winkel α von 37º in Ruhe bleibt? Die Masse der Box beträgt m = 8 kg.
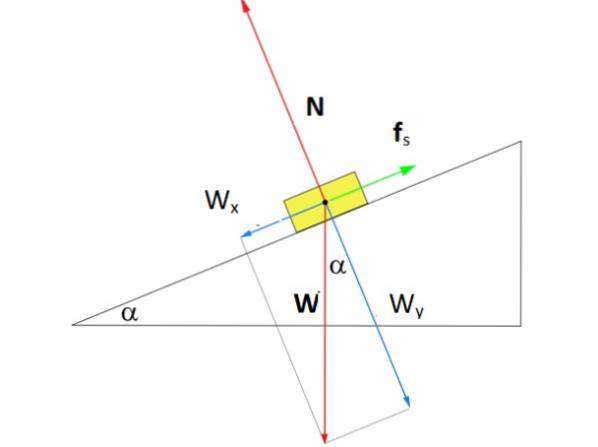
Lösung
Die Abbildung zeigt das Freikörperdiagramm der Box in der Ebene. Es wirken drei Kräfte darauf: Gewicht W., vertikal nach unten gerichtet, die normale N., Dies ist die senkrechte Kraft, die von der Oberfläche der Ebene auf die Box ausgeübt wird, und schließlich die statische Reibungskraft F.s das ist im Gegensatz zu der Box, die bergab rutscht.
Die translatorische Gleichgewichtsbedingung besagt, dass:
W. + N. + F.s = 0
Wir müssen uns jedoch daran erinnern, dass dies eine Vektorsumme ist, und um sie auszuführen, müssen die Kräfte entlang der Koordinatenachsen in Komponenten zerlegt werden.
In der Figur wurde ein Koordinatensystem gezeichnet, bei dem die x-Achse parallel zur Oberfläche der schiefen Ebene verläuft. Bei dieser Wahl fällt die Haftreibung auf die Achse, während die Normale auf der y-Achse liegt. Das Gewicht ist die einzige Kraft, die geneigt ist und mithilfe der Trigonometrie abgebaut werden muss:
W.x = W. sin α
W.Y. = W. cos α
Die Summe der Kräfte entlang jeder Achse ist:
∑ F.Y. = N - W.Y. = 0
∑ F.x = fs - W.x = 0
Aus dieser letzten Gleichung folgt:
F.s = W.x
Und als W.x = W. sin α und die Größe des Gewichts ist wiederum W = m.g, wobei g der Wert der Schwerkraft ist, dann ist die Größe der Haftreibung einfach:
F.s = m⋅g⋅sen α = 8 kg × 9,8 m / szwei × sin 37º = 47,2 N..
Verweise
- Bauer, W. 2011. Physik für Ingenieurwissenschaften. Band 1. Mc Graw Hill.
- Figueroa, D. (2005). Reihe: Physik für Wissenschaft und Technik. Band 2. Dynamik. Herausgegeben von Douglas Figueroa (USB).
- Giambattista, A. 2010. Physik. 2 .. Ed. McGraw Hill.
- Serway, R., Jewett, J. (2008). Physik für Wissenschaft und Technik. Band 1. 7ma. Ed. Lernen einbinden.
- Tippens, P. 2011. Physik: Konzepte und Anwendungen. 7. Auflage. Mcgraw Hügel.



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.