Eneagon-Eigenschaften, wie man ein Eneagon erstellt, Beispiele

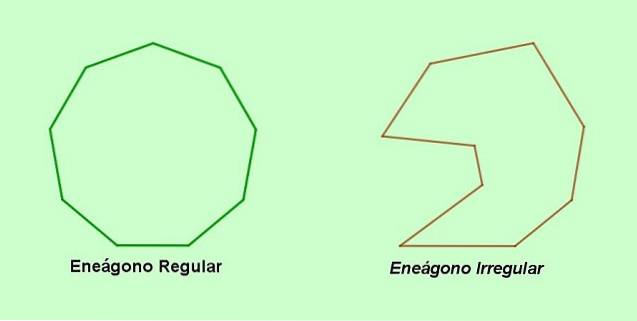
EIN Eneagon ist ein Polygon mit neun Seiten und neun Eckpunkten, die regelmäßig sein können oder nicht. Der Name eneágono stammt aus dem Griechischen und setzt sich aus den griechischen Wörtern zusammen Ennea (neun und Gonon (Winkel).

Ein alternativer Name für das neunseitige Polygon ist nonagon, ein Wort, das aus dem Lateinischen stammt nonus (neun und Gonon (Scheitel). Wenn andererseits die Seiten oder Winkel des Enegons ungleich sind, dann haben wir a unregelmäßiger Enegon. Wenn andererseits die neun Seiten und die neun Winkel des Enegons gleich sind, dann ist es a regelmäßige enegon.

Artikelverzeichnis

• 1 Eigenschaften des Enegons
  • 1.1 Regelmäßiger Enegon
  • 1.2 Bereich eines Enegons bekannt die Seite und das Apothem
  • 1.3 Bereich eines bekannten Enegons die Seite
  • 1.4 Umfang des regulären Enegons bekannt seine Seite
  • 1,5 Umfang des Enegons bekannt sein Radius
• 2 Wie erstelle ich ein reguläres Eneagon?
• 3 Beispiele
  • 3.1 Beispiel 1
  • 3.2 Beispiel 2
• 4 Referenzen

Eneagon-Eigenschaften

Für ein Polygon mit n Seiten ist die Summe seiner Innenwinkel:

(n - 2) * 180º

Im Enegon wäre es n = 9, also ist die Summe seiner Innenwinkel:

Sa = (9 - 2) * 180º = 7 * 180º = 1260º

In jedem Polygon beträgt die Anzahl der Diagonalen:

D = n (n - 3) / 2 und im Fall des Enegons haben wir, da n = 9, dann D = 27.

Regelmäßiger Enegon

Im regulären Eneagon oder Nonagon gibt es neun (9) Innenwinkel mit gleichem Maß, daher misst jeder Winkel ein Neuntel der Gesamtsumme der Innenwinkel.

Das Maß für die Innenwinkel eines Enegons beträgt dann 1260º / 9 = 140º.

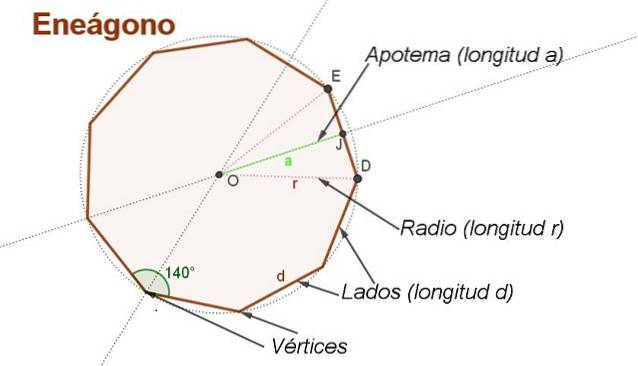
Ableiten der Formel für die Fläche eines regulären Enegons mit Seite d Es ist zweckmäßig, einige Hilfskonstruktionen vorzunehmen, wie die in Abbildung 2 gezeigten.

Das Zentrum befindet sich ODER Verfolgung der Winkelhalbierenden zweier benachbarter Seiten. Das Zentrum ODER äquidistant von den Eckpunkten.

Ein Längenradius r ist das Segment, das von der Mitte ausgeht ODER zu einem Scheitelpunkt des Enegons. Die Radien sind in Abbildung 2 dargestellt. OD Y. OE von Länge r.

Das Apothem ist das Segment, das vom Zentrum zum Mittelpunkt einer Seite des Enegons verläuft. Beispielsweise ABl ist ein Apothem, dessen Länge ist zu.

Bereich eines bekannten Enegons die Seite und das Apothem

Wir betrachten das Dreieck ODE Die Fläche dieses Dreiecks ist das Produkt seiner Basis VON für die Höhe ABl geteilt durch 2:

Bereich ODE = (DE * ABl.) / 2 = (d * a) / 2

Da es im Enegon 9 Dreiecke gleicher Fläche gibt, wird der Schluss gezogen, dass die Fläche desselben ist:

Eneagon Bereich = (9/2) (d * a)

Bereich eines bekannten Enegons die Seite

Wenn nur die Länge d der Seiten des Enegons bekannt ist, muss die Länge des Apothems ermittelt werden, um die Formel aus dem vorherigen Abschnitt anwenden zu können.

Wir betrachten das Dreieck AUGE Rechteck in J. (siehe Abbildung 2). Wenn das tangentiale trigonometrische Tangentenverhältnis angewendet wird, erhalten wir:

so(∡OEJ) = ABl /. Ex.

Der Winkel ∡OEJ = 140º / 2 = 70º, zu sein EO Winkelhalbierende des Innenwinkels des Enegons.

Andererseits, ABl ist das Apothem der Länge zu.

Dann als J. ist der Mittelpunkt von ED es folgt dem EJ = d / 2.

Einsetzen der vorherigen Werte in die Tangentenbeziehung, die wir haben:

tan (70º) = a / (d / 2).

Jetzt klären wir die Länge des Apothems:

a = (d / 2) Bräune (70º).

Das vorherige Ergebnis wird in die Flächenformel eingesetzt, um Folgendes zu erhalten:

Eneagon Bereich = (9/2) (d * a) = (9/2)(( d * (d / 2) Bräune (70º))

Schließlich finden wir die Formel, die es ermöglicht, die Fläche des regulären Enegons zu erhalten, wenn nur die Länge bekannt ist d von seinen Seiten:

Eneagon Bereich = (9/4) d^zwei tan (70º) = 6,1818 d^zwei

Umfang des regulären Enegon bekannt seine Seite

Der Umfang eines Polygons ist die Summe seiner Seiten. Im Falle des Enegons misst jede einzelne Seite eine Länge d, sein Umfang ist die Summe von neun Mal d, nämlich:

Umfang = 9 d

Umfang des Enegons bekannt sein Radius

Betrachtet man das Dreieck AUGE Rechteck in J. (siehe Abbildung 2) wird das trigonometrische Kosinusverhältnis angewendet:

cos (∡OEJ) = Ex /. OE = (d / 2) / r

Woher kommt es:

d = 2r cos (70º)

Wenn wir dieses Ergebnis einsetzen, erhalten wir die Formel für den Umfang als Funktion des Radius des Enegons:

Umfang = 9 d = 18 r cos (70º) = 6,1564 r

Wie man ein regelmäßiges Eneagon macht

1- Um ein reguläres Eneagon mit einem Lineal und einem Kompass zu erstellen, beginnen Sie am Umfang c das umschreibt den Enegon. (siehe Abbildung 3)

2- Zwei senkrechte Linien werden durch die Mitte O des Umfangs gezogen. Dann werden die Schnittpunkte A und B einer der Linien mit dem Umfang markiert.

3- Mit dem Kompass, der am Schnittpunkt B zentriert und gleich dem Radius BO öffnet, wird ein Bogen gezeichnet, der den ursprünglichen Umfang an einem Punkt C abfängt.

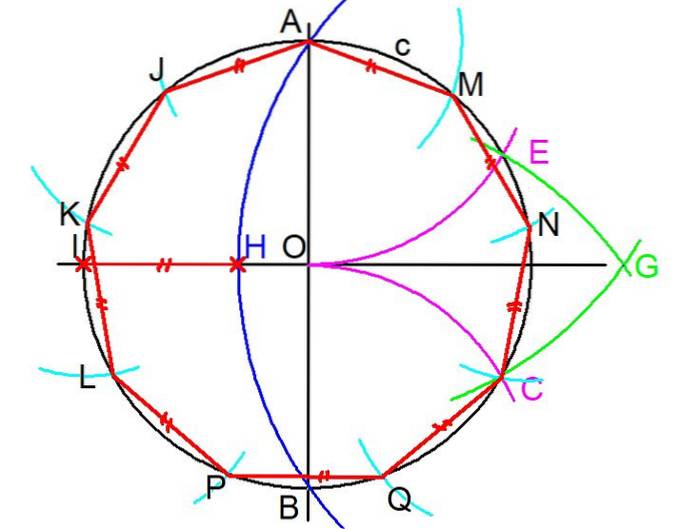
4- Der vorherige Schritt wird wiederholt, wobei jedoch ein Mittelpunkt bei A und der Radius AO gebildet werden. Es wird ein Bogen gezeichnet, der den Umfang c am Punkt E schneidet.

5- Mit der Öffnung AC und der Mitte in A wird ein Umfangsbogen gezeichnet. Ähnlich wird mit der Öffnung BE und der Mitte B ein weiterer Bogen gezeichnet. Der Schnittpunkt dieser beiden Bögen ist als Punkt G markiert.

6- Zentriert bei G und Öffnen von GA wird ein Bogen gezeichnet, der die Sekundärachse (in diesem Fall horizontal) am Punkt H schneidet. Der Schnittpunkt der Sekundärachse mit dem ursprünglichen Umfang c ist mit I markiert.

7- Die Länge des Segments IH ist gleich der Länge d der Seite des Enegons.

8- Mit der Kompassöffnung IH = d werden die Bögen des Radius AJ in der Mitte A, des Radius in der Mitte J, des Radius in der Mitte K, des Radius in der Mitte K und des Radius in der Mitte L nacheinander gezeichnet.

9- In ähnlicher Weise werden ausgehend von A und von der rechten Seite Bögen mit dem Radius IH = d gezeichnet, die die Punkte M, N, C und Q auf dem ursprünglichen Umfang c markieren.

10- Schließlich werden die Segmente AJ, JK, KL, LP, AM, MN, NC, CQ und schließlich PB gezeichnet.

Es ist zu beachten, dass die Bauweise nicht ganz genau ist, da nachgewiesen werden kann, dass die letzte Seite PB 0,7% länger ist als die anderen Seiten. Bisher ist keine Konstruktionsmethode mit einem Lineal und einem Kompass bekannt, die 100% genau sind..

Beispiele

Hier sind einige Beispiele.

Beispiel 1

Sie möchten einen regulären Enegon bauen, dessen Seiten 2 cm messen. Welcher Radius muss den Umfang haben, der ihn umschreibt, damit bei Anwendung der zuvor beschriebenen Konstruktion das gewünschte Ergebnis erzielt wird?

Lösung:

In einem früheren Abschnitt wurde die Formel abgeleitet, die den Radius r des umschriebenen Kreises mit der Seite d eines regulären Enegons in Beziehung setzt:

d = 2r cos (70º)

Wenn wir nach r aus dem vorherigen Ausdruck auflösen, haben wir:

r = d / (2 cos (70º)) = 1,4619 * d

Durch Einsetzen des Wertes d = 2 cm in die vorherige Formel wird ein Radius r von 2,92 cm erhalten.

Beispiel 2

Was ist die Fläche eines regulären Enegons mit einer Seite von 2 cm?

Lösung:

Um diese Frage zu beantworten, müssen wir uns auf die zuvor gezeigte Formel beziehen, die es uns ermöglicht, die Fläche eines bekannten Enegons anhand der Länge d seiner Seite zu finden:

Eneagon Bereich = (9/4) d^zwei tan (70º) = 6,1818 d^zwei

Wenn wir den Wert von 2 cm in der vorherigen Formel durch d ersetzen, erhalten wir:

Eneagon Bereich = 24,72 cm

Verweise

1. C. E. A. (2003). Elemente der Geometrie: mit Übungen und Geometrie des Kompasses. Universität von Medellin.
2. Campos, F., Cerecedo, F. J. (2014). Mathematik 2. Grupo Editorial Patria.
3. Freed, K. (2007). Entdecken Sie Polygone. Benchmark Education Company.
4. Hendrik, V. (2013). Verallgemeinerte Polygone. Birkhäuser.
5. IGER. (s.f.). Mathematik Erstes Semester Tacaná. IGER.
6. Jr. Geometrie. (2014). Polygone. Lulu Press, Inc..
7. Miller, Heeren & Hornsby. (2006). Mathematik: Argumentation und Anwendungen (Zehnte Ausgabe). Pearson Ausbildung.
8. Patiño, M. (2006). Mathematik 5. Editorial Progreso.