Gleichungsformel zweiten Grades, wie man sie löst, Beispiele, Übungen

Das quadratische oder quadratische Gleichungen und ein Unbekannter haben die Form Axt^zwei + bx + c = 0. Wobei a ≠ 0 ist, da wenn es 0 wäre, die Gleichung in eine lineare Gleichung transformiert würde und die Koeffizienten a, b und c reelle Zahlen sind.

Das zu bestimmende Unbekannte ist der Wert von x. Zum Beispiel die Gleichung 3x^zwei - 5x + 2 = 0 ist eine vollständige quadratische Gleichung.

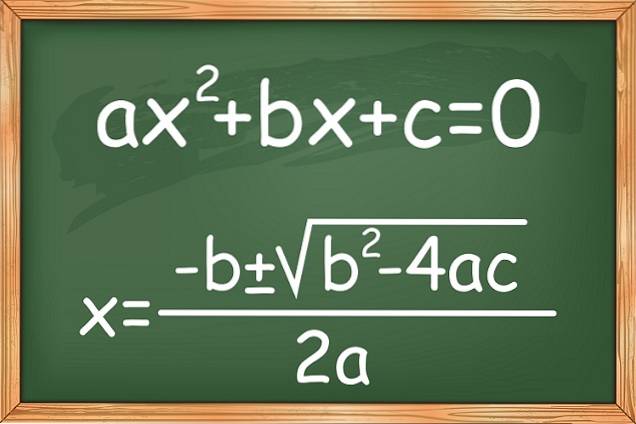
Es gibt auch Varianten, die als unvollständige Gleichungen zweiten Grades bekannt sind und denen keiner der Begriffe außer dem von fehlt Axt^zwei. Hier sind einige Beispiele:

x^zwei - 25 = 0

3x^zwei - 5x = 0

Al Juarismi, der berühmte arabische Mathematiker der Antike, beschrieb in seinen Arbeiten verschiedene Arten von Gleichungen ersten und zweiten Grades, jedoch nur mit positiven Koeffizienten. Es war jedoch der französische Mathematiker Francois Viete, der zuerst Buchstaben einführte, um Mengen zu symbolisieren und die Lösung durch die Formel vorzuschlagen entschlossen::

Dies ist eine allgemeine Formel, die es ermöglicht, eine quadratische Gleichung zu lösen und ihre Wurzeln oder Nullen zu finden, selbst wenn die Lösungen nicht real sind. Es gibt auch andere Möglichkeiten, sie zu lösen.

Artikelverzeichnis

• 1 So lösen Sie quadratische Gleichungen?
  • 1.1 Auflösung durch Factoring
  • 1.2 Grafische Methode
  • 1.3 Auflösung mit wissenschaftlichem Rechner
  • 1.4 Diskriminante einer quadratischen Gleichung
• 2 Beispiele für einfache quadratische Gleichungen
  • 2.1 Gleichung der Form x2 + mx + n = 0
  • 2.2 Unvollständige Gleichung der Form ax2 + c = 0
  • 2.3 Unvollständige Gleichung der Form ax2 + bx = 0
  • 2.4 Gleichungen mit Nenner
  • 2.5 Gleichungen höherer Ordnung, die quadratisch werden
• 3 Einfache gelöste Übungen
  • 3.1 - Übung 1
  • 3.2 - Übung 2
  • 3.3 - Übung 3
• 4 Referenzen

Wie man quadratische Gleichungen löst?

Gleichungen zweiten Grades können durch die oben angegebene Formel gelöst werden, und es gibt auch andere algebraische Verfahren, die zu einigen Gleichungen führen können.

Wir werden die am Anfang vorgeschlagene Gleichung mit der Formel lösen, einer gültigen Methode für jede quadratische Gleichung mit einer unbekannten:

3x^zwei - 5x + 2 = 0

Um die Formel richtig zu verwenden, beachten wir Folgendes:

• zu ist der Koeffizient des Terms mit x^zwei
• b ist der Koeffizient des linearen Terms
• c ist der unabhängige Begriff.

Wir werden sie anhand derselben Gleichung identifizieren:

a = 3

b = -5

c = 2

Beachten Sie, dass das dem Koeffizienten beigefügte Vorzeichen berücksichtigt werden muss. Jetzt ersetzen wir diese Werte in der Formel:

Im Zähler befindet sich das Symbol „Plus - Minus“ ±, das angibt, dass die Menge mit einer Wurzel sowohl als positiv als auch als negativ angesehen werden kann. Eine quadratische Gleichung hat höchstens zwei reelle Lösungen, und dieses Symbol berücksichtigt dies.

Nennen wir x₁ und x_zwei zu diesen beiden Lösungen dann:

x₁ = (5 + 1) / 6 = 1

x_zwei = (5-1) / 6 = 4/6 = 2/3

Auflösung durch Factoring

Einige Gleichungen zweiten Grades bestehen aus Trinomen, die leicht zu berücksichtigen sind. Wenn ja, ist diese Methode viel schneller. Betrachten wir die Gleichung:

x^zwei + 7x - 18 = 0

Die Faktorisierung hat folgende Form:

(x +) ⋅ (x -)

Die Leerzeichen werden mit zwei Zahlen gefüllt, die multipliziert 18 ergeben und subtrahiert 7 ergeben. Die Vorzeichen in Klammern werden mit diesem Kriterium ausgewählt:

-In der ersten Klammer steht das Zeichen zwischen dem ersten und dem zweiten Term.

-Und in der zweiten Klammer steht das Produkt der sichtbaren Zeichen.

Die Zahlen sind in diesem Fall leicht zu bewerten: Sie sind 9 und 2. Die größte Zahl steht immer in der ersten Klammer wie folgt:

x^zwei + 7x - 18 = (x + 9). (x - 2)

Der Leser kann anhand der Verteilungseigenschaft überprüfen, ob bei der Entwicklung des Produkts der rechten Seite der Gleichheit das Trinom der linken Seite erhalten wird. Jetzt wird die Gleichung umgeschrieben:

(x + 9) ⋅ (x - 2) = 0

Damit die Gleichheit erfüllt ist, reicht es aus, dass einer der beiden Faktoren Null ist. Also, im ersten musst du x machen₁ = -9 oder es kann sein, dass der zweite Faktor verschwindet, in welchem ​​Fall x_zwei = 2. Dies sind die Lösungen der Gleichung.

Grafische Methode

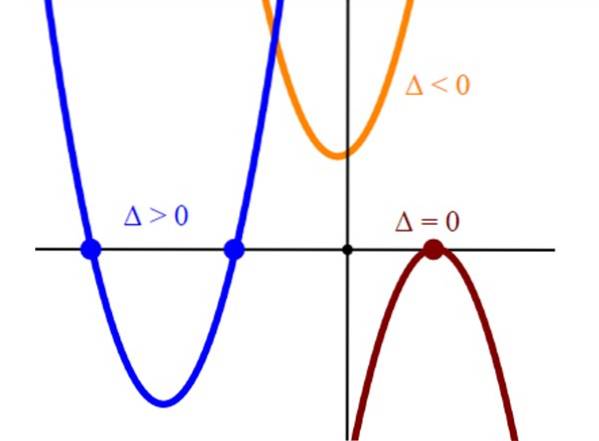
Die Wurzeln oder Lösungen der quadratischen Gleichung entsprechen den Schnittpunkten der Parabel y = Axt^zwei + bx + c mit der horizontalen Achse oder x-Achse. Wenn wir also die entsprechende Parabel grafisch darstellen, finden wir die Lösung der quadratischen Gleichung, indem wir y = 0 machen.

Die Schnitte der Parabeln mit der horizontalen Achse repräsentieren die Lösungen der Gleichung Axt^zwei + bx + c = 0. Eine Parabel, die nur an einem Punkt die horizontale Achse schneidet, hat eine einzige Wurzel und dies ist immer der Scheitelpunkt der Parabel.

Und schließlich, wenn eine Parabel die horizontale Achse nicht schneidet, die entsprechende Gleichung Axt^zwei + bx + c = 0 Es fehlen echte Lösungen.

Das Erstellen eines Diagramms von Hand kann mühsam sein, aber mit der Verwendung von Programmen, die online Diagramme erstellen, ist dies sehr einfach.

Auflösung mit wissenschaftlichem Rechner

Viele Modelle wissenschaftlicher Taschenrechner bieten die Möglichkeit, quadratische Gleichungen (und auch andere Arten von Gleichungen) zu lösen. Um dies herauszufinden, müssen Sie das Menü überprüfen.

Sobald die quadratische Gleichung einer unbekannten Option ausgewählt ist, werden Sie aufgefordert, die Werte der Koeffizienten a, b und c einzugeben, und geben die tatsächlichen Lösungen zurück, falls vorhanden. Und es gibt auch Modelle wissenschaftlicher Taschenrechner, die mit komplexen Zahlen arbeiten und diese Lösungen anbieten.

Diskriminante einer quadratischen Gleichung

Um herauszufinden, ob die Gleichung reale Lösungen hat oder nicht und wie viele es gibt, ohne zuerst lösen zu müssen, wird die Diskriminante Δ als die Größe unter der Quadratwurzel definiert:

Δ = b^zwei - 4ac

Nach dem Vorzeichen der Diskriminante ist bekannt, wie viele Lösungen die Gleichung nach diesem Kriterium hat:

-Zwei reale Lösungen: Δ> 0

-Eine reale Lösung (oder zwei identische Lösungen): Δ = 0

-Keine wirkliche Lösung: Δ  < 0

Zum Beispiel, wie viele Lösungen hat die quadratische Gleichung -7x^zwei +12x + 64 = 0? Wir identifizieren die Koeffizienten:

a = -7

b = 12

c = 64

Δ = b^zwei - 4ac = 12^zwei - 4x (-7) x 64 = 144 + 1792 = 1936> 0

Die Gleichung hat zwei Lösungen. Nun sehen wir uns diesen anderen an:

x^zwei - 6x + 9 = 0

a = 1

b = -6

c = 9

Δ = (-6)^zwei - 4 x 1 x 9 = 36 - 36 = 0

Dies ist eine Gleichung mit einer einzelnen Lösung oder mit zwei gleichen Lösungen.

Beispiele für einfache quadratische Gleichungen

Zu Beginn sagten wir, dass Gleichungen zweiten Grades vollständig sein könnten, wenn das Trinom vorliegt, und unvollständig, wenn der lineare Term oder der unabhängige Term fehlen. Schauen wir uns nun einige bestimmte Typen an:

Gleichung der Form x^zwei + mx + n = 0

In diesem Fall ist a = 1 und die Formel reduziert sich auf:

Für diese Art von Gleichung und immer abhängig von den verbleibenden Koeffizienten kann die Factoring-Methode gut funktionieren, wie wir im vorherigen Abschnitt gesehen haben.

Unvollständige Gleichung der Form ax^zwei + c = 0

Die Lösung, falls vorhanden, hat folgende Form:

Es gibt eine echte Lösung, wenn a oder c ein negatives Vorzeichen haben, aber wenn die beiden Terme das gleiche Vorzeichen haben, ist die Lösung imaginär.

Unvollständige Gleichung der Form ax^zwei + bx = 0

Diese Gleichung wird durch Factoring schnell gelöst, da x in beiden Begriffen ein gemeinsamer Faktor ist. Eine der Lösungen ist immer x = 0, die andere lautet wie folgt:

Axt^zwei + bx = 0

x (ax + b) = 0

ax + b = 0 → x = -b / a

Sehen wir uns unten ein Beispiel an. Aussortieren:

x^zwei - 5x = 0

x (x - 5) = 0

Deshalb x₁ = 0 und x_zwei = 5

Gleichungen mit Nenner

Es gibt verschiedene Gleichungen eines rationalen Typs, bei denen das Unbekannte sowohl im Zähler als auch im Nenner oder sogar nur im letzteren vorhanden sein kann und die durch algebraische Manipulationen auf quadratische Gleichungen reduziert werden.

Der Weg, sie zu lösen, besteht darin, beide Seiten der Gleichheit mit dem kleinsten gemeinsamen Vielfachen oder m.c.m der Nenner zu multiplizieren und dann die Terme neu anzuordnen. Beispielsweise:

Gleichungen höherer Ordnung, die quadratisch werden

Es gibt Gleichungen höherer Ordnung, die gelöst werden können, als ob sie durch eine Änderung der Variablen quadratisch wären, zum Beispiel diese Gleichung Bi-Quadrat::

x⁴ - 10x^zwei + 9 = 0

Sei x^zwei = u, dann wird die Gleichung:

oder^zwei - 10u + 9 = 0

Diese Gleichung wird schnell durch Faktorisierung gelöst, wobei zwei Zahlen gefunden werden, die mit 9 multipliziert und 10 addiert werden. Diese Zahlen sind 9 und 1:

(u - 9). (u - 1) = 0

Daher sind die Lösungen dieser Gleichung u₁ = 9 und u_zwei = 1. Jetzt geben wir die Änderung zurück:

x^zwei = 9 → x₁ = 3 und x_zwei = -3

x^zwei = 1 → x₁ = 1 und x_zwei = -1

Die ursprüngliche Gleichung hat die Ordnung 4, daher hat sie mindestens 4 Wurzeln. Die im Beispiel ist -3, -1, 1 und 3.

Einfache gelöste Übungen

- Übung 1

Lösen Sie die folgende quadratische Gleichung mit dem Unbekannten im Nenner:

Das am wenigsten verbreitete Vielfache ist x (x + 2) und Sie müssen alle Begriffe multiplizieren:

Der äquivalente Ausdruck bleibt:

5x (x + 2) - x = x (x + 2)

Wir entwickeln:

5x^zwei + 10x - x = x^zwei + 2x

Alle Begriffe werden links von der Gleichheit transponiert und rechts verlassen wir 0:

5x^zwei + 10x - x - x^zwei - 2x = 0

4x^zwei - 7x = 0

Wir berücksichtigen, da es sich um eine unvollständige Gleichung handelt:

x (4x - 7) = 0

Eine der Lösungen ist x = 0, die andere ist:

4x = 7

x = 7/4

- Übung 2

Finden Sie die Lösung der quadratischen Gleichungen:

a) -7x^zwei +12x + 64 = 0

b) x^zwei - 6x + 9 = 0

Lösung für

Aus dieser Gleichung kennen wir die Determinante Δ, da sie zuvor als Beispiel berechnet wurde. Wir werden sie also nutzen und die Auflösungsformel wie folgt ausdrücken:

x₁ = (-12 + 44) / -14 = - (32/14) = - (16/7)

x_zwei = (-12 - 44) / -14 = 4

Lösung b

Das quadratische Trinom x^zwei - 6x + 9 ist faktorisierbar, da es sich um ein perfektes quadratisches Trinom handelt:

x^zwei - 6x + 9 = (x-3)^zwei = 0

Die Lösung für diese Gleichung lautet x = 3.

- Übung 3

Was ist die Gleichung, deren Lösungen 3 und 4 sind?

Lösung

Der faktorisierte Ausdruck lautet:

(x - 3) ⋅ (x - 4) = 0

Verteilungseigenschaft anwenden:

x^zwei - 4x -3x + 12 = 0

Die beiden zentralen Begriffe sind ähnlich und können reduziert werden, so dass:

x^zwei - 7x + 12 = 0

Verweise

1. Baldor. 1977. Elementare Algebra. Venezolanische Kulturausgaben.
2. Hoffman, J. Auswahl mathematischer Themen. Band 2.
3. Jiménez, R. 2008. Algebra. Prentice Halle.
4. Stewart, J. 2006. Precalculus: Mathematik für Calculus. 5 .. Auflage. Lernen einbinden.
5. Zapata, F. 4 Möglichkeiten, eine quadratische Gleichung zu lösen. Wiederhergestellt von: francesphysics.blogspot.com.
6. Zill, D. 1984. Algebra und Trigonometrie. Mcgraw Hügel.