Synthetische Teilungsmethode und gelöste Übungen

Das Synthetische Abteilung ist eine einfache Möglichkeit, ein Polynom P (x) durch eine der Formen d (x) = x - c zu teilen. Zum Beispiel ist das Polynom P (x) = (x⁵+3x⁴-7x³+2x^zwei-8x + 1) kann als Multiplikation der beiden einfachsten Polynome (x + 1) und (x) dargestellt werden⁴ + 2x³).

Es ist ein sehr nützliches Werkzeug, da wir nicht nur Polynome teilen können, sondern auch ein Polynom P (x) bei einer beliebigen Zahl c auswerten können, was uns wiederum genau sagt, ob diese Zahl eine Null ist oder nicht Polynom.

Dank des Divisionsalgorithmus wissen wir, dass wir zwei Polynome haben P (x) Y. d (x) Nichtkonstanten gibt es Polynome q (x) Y. r (x) eindeutige, so dass es gilt, dass P (x) = q (x) d (x) + r (x), wobei r (x) Null oder weniger als q (x) ist. Diese Polynome sind als Quotient und Rest bzw. Rest bekannt.

In den Fällen, in denen das Polynom d (x) die Form x-c hat, gibt uns die synthetische Division eine kurze Möglichkeit, herauszufinden, wer q (x) und r (x) sind..

Artikelverzeichnis

• 1 Synthetische Teilungsmethode
• 2 Gelöste Übungen
  • 2.1 - Beispiel 1
  • 2.2 - Beispiel 2
  • 2.3 - Beispiel 3
  • 2.4 - Beispiel 4
• 3 Referenzen

Synthetische Teilungsmethode

Sei P (x) = a_nxⁿ+zu_n-1x^n-1+… + A.₁x + a₀ das Polynom, das wir teilen wollen und d (x) = x-c der Divisor. Um durch die synthetische Teilungsmethode zu teilen, gehen wir wie folgt vor:

1- Wir schreiben die Koeffizienten von P (x) in die erste Zeile. Wenn eine Potenz von X nicht erscheint, setzen wir Null als Koeffizienten.

2- In der zweiten Reihe links von a_n Wir platzieren c und zeichnen Trennlinien wie in der folgenden Abbildung gezeigt:

3- Wir senken den Leitkoeffizienten auf die dritte Reihe.

In diesem Ausdruck b_n-1= a_n

4- Wir multiplizieren c mit dem führenden Koeffizienten b_n-1 und wir schreiben das Ergebnis in die zweite Zeile, aber eine Spalte nach rechts.

5- Wir fügen die Spalte hinzu, in die wir das vorherige Ergebnis schreiben, und platzieren das Ergebnis unter dieser Summe. das heißt, in derselben Spalte, dritte Zeile.

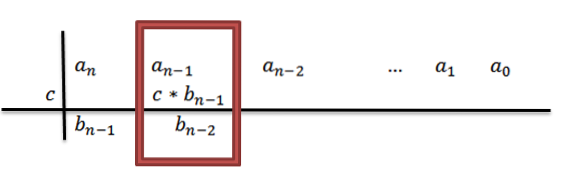
Beim Hinzufügen haben wir als Ergebnis_n-1+c * b_n-1, was wir der Einfachheit halber nennen werden b_n-2

6- Wir multiplizieren c mit dem vorherigen Ergebnis und schreiben das Ergebnis rechts in die zweite Zeile.

7- Wir wiederholen die Schritte 5 und 6, bis wir den Koeffizienten a erreichen₀.

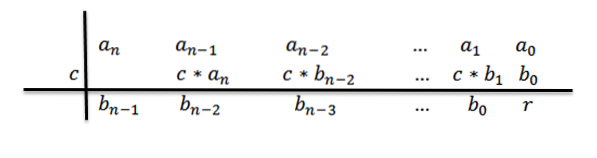
8- Wir schreiben die Antwort; das heißt, der Quotient und der Rest. Da wir ein Polynom vom Grad n durch ein Polynom vom Grad 1 teilen, haben wir, dass der Quotient vom Grad n-1 wäre.

Die Koeffizienten des Quotientenpolynoms sind die Zahlen in der dritten Reihe mit Ausnahme der letzten, die der Rest oder der Rest der Division ist.

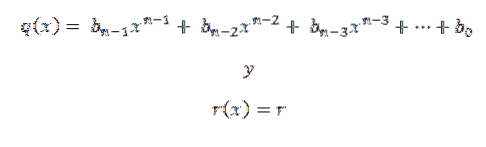
Gelöste Übungen

- Beispiel 1

Führen Sie die folgende Division nach der synthetischen Divisionsmethode durch:

(x⁵+3x⁴-7x³+2x^zwei-8x + 1): (x + 1).

Lösung

Wir schreiben zuerst die Dividendenkoeffizienten wie folgt:

Dann schreiben wir c auf die linke Seite in der zweiten Reihe zusammen mit den Trennlinien. In diesem Beispiel ist c = -1.

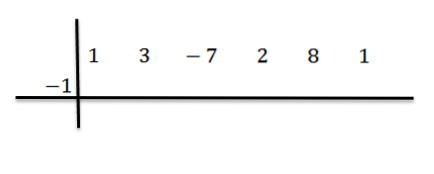
Wir senken den Leitkoeffizienten (in diesem Fall b_n-1 = 1) und wir multiplizieren es mit -1:

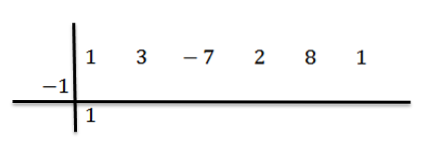
Wir schreiben das Ergebnis rechts in die zweite Zeile, wie unten gezeigt:

Wir fügen die Zahlen in der zweiten Spalte hinzu:

Wir multiplizieren 2 mit -1 und schreiben das Ergebnis in die dritte Spalte, zweite Zeile:

Wir fügen in der dritten Spalte hinzu:

Wir gehen genauso vor, bis wir die letzte Spalte erreichen:

Wir haben also, dass die zuletzt erhaltene Zahl der Rest der Division ist und die verbleibenden Zahlen die Koeffizienten des Quotientenpolynoms sind. Dies ist wie folgt geschrieben:

Wenn wir überprüfen möchten, ob das Ergebnis korrekt ist, reicht es aus, um zu überprüfen, ob die folgende Gleichung wahr ist:

P (x) = q (x) · d (x) + r (x)

So können wir überprüfen, ob das erhaltene Ergebnis korrekt ist.

- Beispiel 2

Führen Sie die folgende Division von Polynomen nach der Methode der synthetischen Division durch

(7x³-x + 2): (x + 2)

Lösung

In diesem Fall haben wir den Term x^zwei es erscheint nicht, also schreiben wir 0 als Koeffizienten. Somit wäre das Polynom 7x³+0x^zwei-x + 2.

Wir schreiben ihre Koeffizienten in einer Reihe, dies ist:

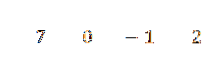
Wir schreiben den Wert von C = -2 auf die linke Seite in die zweite Zeile und zeichnen die Trennlinien.

Wir senken den Leitkoeffizienten b_n-1 = 7 und multipliziere es mit -2, indem du dein Ergebnis in die zweite Zeile rechts schreibst.

Wir fügen hinzu und fahren wie zuvor erläutert fort, bis wir den letzten Begriff erreichen:

In diesem Fall ist der Rest r (x) = - 52 und der erhaltene Quotient ist q (x) = 7x^zwei-14x + 27.

- Beispiel 3

Eine andere Möglichkeit, die synthetische Division zu verwenden, ist die folgende: Nehmen wir an, wir haben ein Polynom P (x) vom Grad n und möchten wissen, was ein Wert ist, indem wir ihn bei x = c bewerten.

Durch den Divisionsalgorithmus können wir das Polynom P (x) wie folgt schreiben:

In diesem Ausdruck sind q (x) und r (x) der Quotient bzw. der Rest. Wenn nun d (x) = x - c ist, erhalten wir bei der Auswertung bei c im Polynom Folgendes:

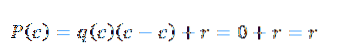
Aus diesem Grund bleibt nur r (x) zu finden, und wir können dies dank der synthetischen Teilung tun.

Zum Beispiel haben wir das Polynom P (x) = x⁷-9x⁶+19x⁵+12x⁴-3x³+19x^zwei-37x-37 und wir wollen wissen, was sein Wert ist, indem wir ihn bei x = 5 bewerten. Um dies zu tun, teilen wir zwischen P (x) und d (x) = x -5 durch die synthetische Teilungsmethode:

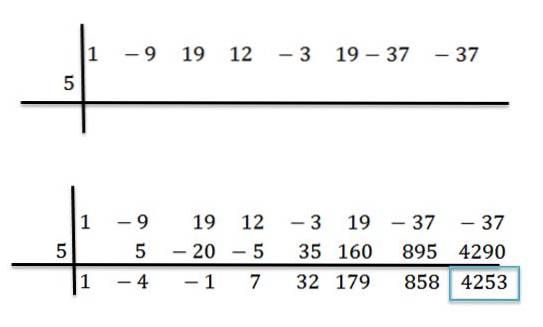
Sobald die Operationen abgeschlossen sind, wissen wir, dass wir P (x) auf folgende Weise schreiben können:

P (x) = (x⁶-4x⁵ -x⁴+ 7x³ +32x^zwei +179x + 858) * (x-5) + 4253

Daher müssen wir bei der Bewertung:

P (5) = (5-4 (5) -5 + 7 (5) +32 (5) +179 (5) +858) * (5-5) + 4253

P (5) = (5-4 (5) -5 + 7 (5) +32 (5) +179 (5) +858) * (0) + 4253

P (5) = 0 + 4253 = 4253

Wie wir sehen können, ist es möglich, die synthetische Division zu verwenden, um den Wert eines Polynoms zu ermitteln, indem es bei c ausgewertet wird, anstatt einfach x durch c zu ersetzen. 

Wenn wir versuchen würden, P (5) auf herkömmliche Weise zu bewerten, wären wir gezwungen, einige Berechnungen durchzuführen, die tendenziell langweilig werden.

- Beispiel 4

Der Divisionsalgorithmus für Polynome gilt auch für Polynome mit komplexen Koeffizienten. Infolgedessen funktioniert die synthetische Divisionsmethode auch für solche Polynome. Als nächstes sehen wir ein Beispiel.

Wir werden die synthetische Teilungsmethode verwenden, um zu zeigen, dass z = 1+ 2i eine Null des Polynoms P (x) = x ist³+ (1 + i) x^zwei -(1 + 2i) x + (15 + 5i); das heißt, der Rest der Division P (x) durch d (x) = x - z ist gleich Null.

Wir gehen wie zuvor vor: In der ersten Zeile schreiben wir die Koeffizienten von P (x), in der zweiten schreiben wir z und zeichnen die Teilungslinien.

Wir führen die Teilung wie zuvor durch; das ist:

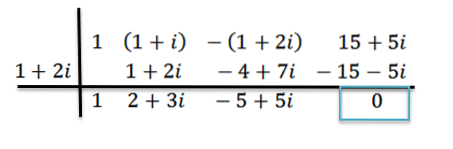
Wir können sehen, dass der Rest Null ist; daher schließen wir, dass z = 1+ 2i eine Null von P (x) ist.

Verweise

1. Baldor aurelio. Algebra. Grupo Editorial Patria.
2. Demana, Waits, Foley & Kennedy. Precalculus: Grafisch, numerisch, algebraisch 7. Aufl. Pearson Education.
3. Flemming W & Varserg D. Algebra und Trigonometrie mit analytischer Geometrie. Prentice Halle
4. Michael Sullivan. Vorberechnung 4th Ed. Pearson Ausbildung.
5. Rot. Armando O.. Algebra 1 6. Aufl. Das Athenaeum.