
Dynamik eines Systems von Partikeln Beispiele, Übungen
Das Dynamik eines Partikelsystems Es besteht aus der Anwendung der Newtonschen Bewegungsgesetze auf eine Reihe von Partikeln, die diskret sein können (die Partikel können gezählt werden) oder Teil eines erweiterten Objekts sind. In diesem Fall ist das System kontinuierlich.
Um die Bewegung eines Partikelsystems zu erklären, ist es unpraktisch, jedes einzeln zu analysieren und zu sehen, welche Kräfte auf es wirken. Stattdessen wird ein repräsentativer Punkt der Menge definiert, der als Massenzentrum.
Die Beschreibung der Bewegung des Massenschwerpunkts bietet einen sehr genauen Überblick über die Gesamtbewegung des Ganzen und ermöglicht auch die analoge Anwendung der Newtonschen Gesetze, wenn das Objekt als dimensionsloses Teilchen betrachtet wird.
Dieses neueste Modell heißt Teilchenmodell, Es ist gut für die Beschreibung von Übersetzungen und auch dann, wenn Sie die Abmessungen des Objekts nicht berücksichtigen müssen. Gewöhnliche Objekte haben jedoch eine Größe, und wenn sie auch eine Rotationsbewegung haben, müssen die Punkte berücksichtigt werden, auf die die Kräfte ausgeübt werden.
Artikelverzeichnis
- 1 Beispiele
- 1.1 Die Erde und der Mond
- 1.2 Erweiterte Objekte
- 2 Der Schwerpunkt eines Partikelsystems
- 2.1 CM Bewegung
- 2.2 Kraft auf CM ausüben
- 3 Übung gelöst
- 3.1 Lösung a
- 3.2 Lösung b
- 3.3 Lösung c
- 4 Referenzen
Beispiele
Die Erde und der Mond

Eine Reihe von diskreten Partikeln m1, mzwei, m3... das sich aufgrund einer auf sie einwirkenden Kraft schließlich in Bezug auf den Ursprung eines Koordinatensystems bewegt, ist ein gutes Beispiel für ein Partikelsystem.
Die Erde kann als ein Teilchen und der Mond als ein anderes betrachtet werden, dann bilden beide ein System von 2 Teilchen unter der Wirkung der Schwerkraft der Sonne..
Erweiterte Objekte
Eine Person, ein Tier oder ein Gegenstand in der Umwelt kann auch als Partikelsystem betrachtet werden, nur dass diese so klein sind, dass sie nicht einzeln gezählt werden können. Dies ist ein kontinuierliches System, aber unter Berücksichtigung bestimmter Überlegungen ist seine Behandlung dieselbe wie bei einem diskreten System.
Unten sind die Details.
Der Schwerpunkt eines Partikelsystems
Um mit der Untersuchung eines Partikelsystems zu beginnen, müssen wir den Schwerpunkt (CM) finden, der der Punkt ist, an dem die gesamte Masse des Systems konzentriert ist..
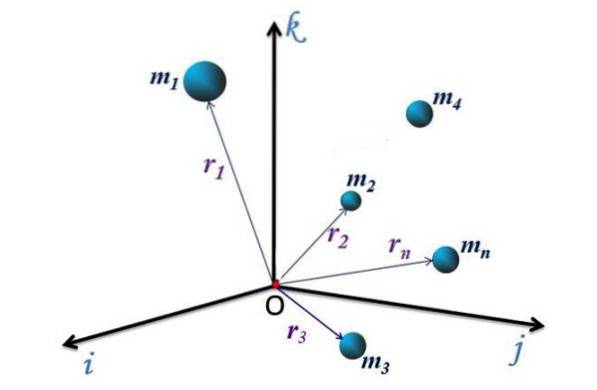
Für das diskrete System von 1 mit n Teilchen, jedes hat einen Positionsvektor, der vom Ursprung O des Koordinatensystems zu dem Punkt P (x, y, z) gerichtet ist, an dem sich das Teilchen befindet. Diese Vektoren werden als bezeichnet r1, rzwei, r3... rn.
Die Koordinaten des CM werden unter Verwendung der folgenden Gleichungen berechnet:

Wobei jede der Massen der Menge als m dargestellt wird1, mzwei, m3... mn. Beachten Sie, dass die Summe ∑ mich entspricht der Gesamtmasse M der Baugruppe. Wenn das System kontinuierlich ist, werden die Summierungen durch Integrale ersetzt.
Jede der senkrechten Richtungen wird durch die Einheitsvektoren dargestellt ich, j Y. k, daher wird der Positionsvektor des CM bezeichnet rCM, kann ausgedrückt werden durch:
rCM = xCM ich + Y.CM j + zCM k
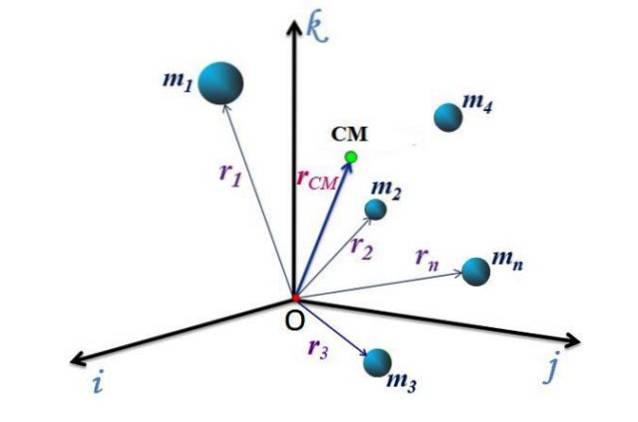
CM Bewegung
Sobald der Ort des Massenschwerpunkts bekannt ist, gelten die bekannten Bewegungsgleichungen. Die Geschwindigkeit des CM ist die erste Ableitung der Position in Bezug auf die Zeit:

In diesem Fall hat das System einen Gesamtimpuls P. welches als Produkt der Gesamtmasse des Systems und der Geschwindigkeit des Massenschwerpunkts berechnet wird:
P. = M ∙vCM
Alternativ kann der Gesamtimpuls des Systems direkt berechnet werden:
P. = m1v1 + mzweivzwei + m3v3 +…. = ∑ mich vich
Während die Beschleunigung des CM die Ableitung der Geschwindigkeit ist:

Kraft auf CM
Die auf ein Partikelsystem einwirkenden Kräfte können sein:
- Schnittgrößen aufgrund von Wechselwirkungen zwischen denselben Partikeln.
- Externe Kräfte, die von Agenten außerhalb des Systems verursacht werden.
Da die inneren Kräfte paarweise dargestellt werden, von gleicher Größe und Richtung, aber entgegengesetzten Richtungen, ist es nach dem dritten Newtonschen Gesetz wahr, dass:
∑ F.int = 0
Daher verändern die inneren Kräfte nicht die Bewegung des Ganzen, aber sie sind sehr wichtig, um die innere Energie zu bestimmen..
Wenn das System isoliert ist und keine äußeren Kräfte vorhanden sind, befindet sich der Schwerpunkt nach Newtons erstem Gesetz in Ruhe oder bewegt sich mit gleichmäßiger geradliniger Bewegung. Andernfalls erfährt der Schwerpunkt eine Beschleunigung, die gegeben ist durch:
∑ F.ext = M ∙zuCM
Wobei M die Gesamtmasse des Systems ist. Die obige Gleichung kann folgendermaßen geschrieben werden:

Und es bedeutet, dass die äußere Kraft der zeitlichen Variation des Impulses entspricht, einer anderen Art, Newtons zweites Gesetz auszudrücken, und der gleichen, die der berühmte englische Physiker in seinem Buch verwendet hat Prinzip.
Übung gelöst
Der Schwerpunkt eines 2-Teilchen-Systems liegt zu einem bestimmten Zeitpunkt auf der x-Achse, an der Position x = 2,0 m und bewegt sich mit einer Geschwindigkeit von 5,0 m / s in die gleiche Richtung und in die positive Richtung. Befindet sich eines der Partikel am Ursprung und das andere mit einer Masse von 0,1 kg in Ruhe bei x = 8,0 m, berechnen Sie:
a) Die Masse des Partikels, die sich am Ursprung befindet.
b) Bewegungsumfang des Systems
c) Wie schnell ist das Teilchen am Ursprung??
Lösung für
Aus der Gleichung für die Position des Massenschwerpunkts:
rCM = xCM ich + Y.CM j + zCM k = 2,0 m ich
Da das CM nur eine x-Koordinate hat, wird nur die erste Gleichung des zuvor angegebenen Trios verwendet:

Jetzt werden die Koordinaten ersetzt. Wenn das Teilchen am Ursprung als Nummer 1 und das andere als Nummer 2 bezeichnet wird, sind die numerischen Daten:
x1 = 0 m, xzwei = 8,0 m, mzwei = 0,1 kg, xCM = 2,0 m
Verbleibend:

Lösung b
Das Ausmaß der Bewegung des Systems wird berechnet durch:
P. = M ∙vCM
Die Gesamtmasse M ist gleich:
M = 0,3 kg + 0,1 kg = 0,4 kg
Deshalb:
P. = 0,4 kg ≤ 5,0 m / s ich = 2 kg.m / s ich
Lösung c
Aus der Gleichung für P. eines Zwei-Teilchen-Systems klärt es v1, da die anderen Daten bekannt sind, da die Aussage besagt, dass Partikel 2 in Ruhe ist, daher:
vzwei = 0
Y. P. es sieht einfach so aus:
P. = m1v1
v1 = P. / m1 = 2 kg.m / s ich / 0,3 kg = 6,67 m / s ich
Verweise
- Duke University. Partikelsysteme. Wiederhergestellt von: webhome.phy.duke.edu.
- Rex, A. 2011. Grundlagen der Physik. Pearson.
- Sears, Zemansky. 2016. Universitätsphysik mit moderner Physik. 14 .. Ed. Band 1. Pearson.
- Serway, R., Jewett, J. (2008). Physik für Wissenschaft und Technik. Band 1. 7 .. Ed. Lernen einbinden.
- Tipler, P. (2006) Physik für Wissenschaft und Technologie. 5. Aufl. Band 1. Editorial Reverté.



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.