
Was sind die Elemente des Gleichnisses? (Teile)

Das Parabelelemente Sie sind die Achse, der Fokus, die Gerade, der Parameter, der Scheitelpunkt, die Brennweite, der Akkord, der Brennakkord, die gerade Seite und ihre Punkte.
Dank dieser Elemente oder Teile können Längen und Eigenschaften der Parabeln berechnet werden. Die Hauptkomponenten, aus denen alle anderen Elemente hervorgehen, sind die Achse, die Gerade und der Fokus..
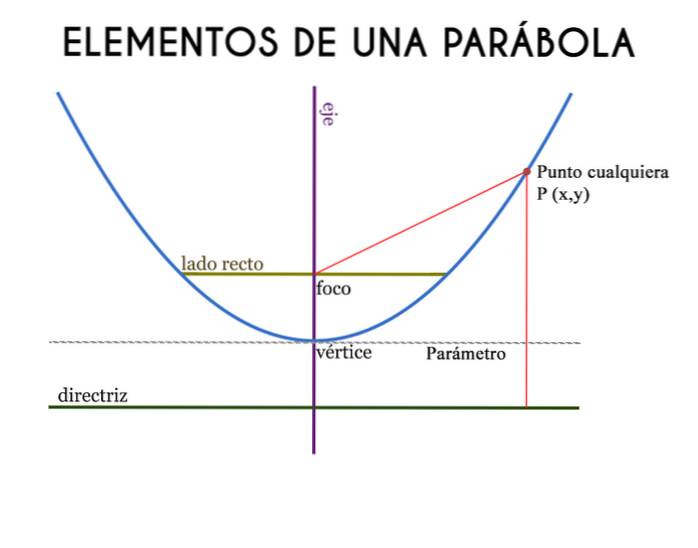
Eine Parabel ist eine gekrümmte Linie, deren Punkte gleich weit von einem Fokus auf der Innenseite der Kurve entfernt sind, und eine Linie, die als Directrix bezeichnet wird und sich außen und senkrecht zur Parabel befindet. Geometrisch entspricht es einem Kegelschnitt mit einer Exzentrizität von 1.
Die Elemente, aus denen eine Parabel besteht
Da alle Parabeln einem Kegelschnitt mit derselben Exzentrizität entsprechen, sind auf geometrischer Ebene alle Parabeln ähnlich, und der einzige Unterschied zwischen den beiden besteht in der Skala, mit der sie arbeiten..
Normalerweise werden Parabeln während des Studiums der Mathematik, Physik und Geometrie von Hand gezeichnet, ohne einige Parameter zu berücksichtigen. Aus diesem Grund scheinen die meisten Parabeln eine andere Form oder einen anderen Winkel zu haben..
Die drei Hauptelemente, aus denen eine Parabel besteht, sind der Fokus, die Achse und die Gerade. Die Achse und die Gerade sind senkrechte Linien, die sich schneiden, während der Fokus ein Punkt auf der Achse ist..
Die Parabel bildet eine gekrümmte Linie zwischen dem Fokus und der Geraden, alle Punkte der Parabel sind vom Fokus und der Geraden gleich weit entfernt.
1- Fokus
Es ist ein Punkt auf der Achse, jeder Punkt der Parabel befindet sich im gleichen Abstand vom Fokus und der Geraden.
2- Achse
Es ist die symmetrische Achse der Parabel. Der Punkt, an dem die Achse die Parabel schneidet, wird als Scheitelpunkt bezeichnet.
3- Richtlinie
Die Directrix ist eine Linie senkrecht zur Achse ablehnen zum Gleichnis. Wenn Sie sich an einem beliebigen Punkt der Parabel befinden, um eine Linie zum Fokus zu zeichnen, entspricht ihre Länge einer Linie, die zur Geraden gezogen wird.
4- Parameter
Es ist eine Linie senkrecht zur Geraden und parallel zur Achse, die einen Vektor zwischen dem Fokus und der Geraden bildet.
5- Scheitelpunkt
Entspricht dem Schnittpunkt, an dem sich Achse und Parabel schneiden. Der Scheitelpunkt einer Parabel befindet sich in der Mitte zwischen Fokus und Directrix.
6- Brennweite
Dies ist der Abstand zwischen dem Fokus und dem Scheitelpunkt. Dies entspricht dem Wert des Parameters geteilt durch 2.
7- Seil
Ein Akkord ist eine gerade Linie, die zwei Punkte einer Parabel verbindet.
8- Fokuskabel
Es ist ein Akkord, der zwei Punkte einer Parabel verbindet, die durch den Fokus geht.
9- Gerade Seite
Die gerade Seite ist ein Fokusakkord parallel zur Geraden und senkrecht zur Achse. Sein Wert entspricht dem doppelten Parameter.
10 Punkte
Beim Zeichnen einer Parabel werden auf beiden Seiten der Kurve 2 recht differenzierbare Räume gebildet. Diese beiden Seiten bilden den inneren und äußeren Punkt der Parabel.
Innenpunkte sind alle Punkte, die sich auf der Innenseite der Kurve befinden. Die äußeren Punkte sind diejenigen, die sich im äußeren Teil zwischen der Parabel und der Geraden befinden.
Verweise
- Parabel (s.f.). Abgerufen am 10. Dezember 2017 von Mathwords.
- Definition und Elemente des Gleichnisses (s.f.). Abgerufen am 10. Dezember 2017 von Sangakoo.
- Parabel (s.f.). Abgerufen am 10. Dezember 2017 von Vitutor.
- Elemente eines Gleichnisses (s.f.). Abgerufen am 10. Dezember 2017 von der Universo Fórmula.
- Parabel (s.f.). Abgerufen am 10. Dezember 2017 von Math macht Spaß.


Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.