Was ist der Rand eines Würfels?

Das Rand eines Würfels Es ist eine Kante davon: Es ist die Linie, die zwei Eckpunkte oder Ecken verbindet. Eine Kante ist die Linie, an der sich zwei Flächen einer geometrischen Figur schneiden.

Die obige Definition ist allgemein und gilt für jede geometrische Figur, nicht nur für den Würfel. Wenn es sich um eine flache Figur handelt, entsprechen die Kanten den Seiten dieser Figur.

Parallelepiped wird als geometrische Figur mit sechs Flächen in Form von Parallelogrammen bezeichnet, von denen die gegenüberliegenden gleich und parallel sind..

In dem speziellen Fall, in dem die Flächen quadratisch sind, wird das Parallelepiped als Würfel oder Hexaeder bezeichnet, eine Figur, die als reguläres Polyeder betrachtet wird..

Möglichkeiten, die Kanten eines Würfels zu identifizieren

Zur besseren Veranschaulichung können Alltagsgegenstände verwendet werden, um die Kanten eines Würfels genau zu bestimmen.

1- Zusammenbau eines Papierwürfels

Wenn Sie sich ansehen, wie ein Papier- oder Pappwürfel aufgebaut ist, können Sie seine Kanten erkennen. Sie zeichnen zunächst ein Kreuz wie das in der Abbildung und markieren bestimmte Linien darin.

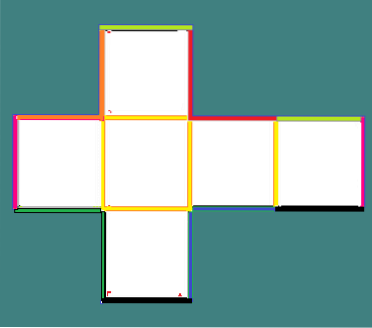
Jede der gelben Linien stellt eine Falte dar, die eine Kante des Würfels (Kante) darstellt..

In ähnlicher Weise bildet jedes Linienpaar mit derselben Farbe beim Verbinden eine Kante. Insgesamt hat ein Würfel 12 Kanten.

2- Einen Würfel zeichnen

Eine andere Möglichkeit, die Kanten eines Würfels zu erkennen, besteht darin, zu beobachten, wie er gezeichnet wird. Wir beginnen mit dem Zeichnen eines Quadrats mit Seite L; Jede Seite des Quadrats ist eine Kante des Würfels.

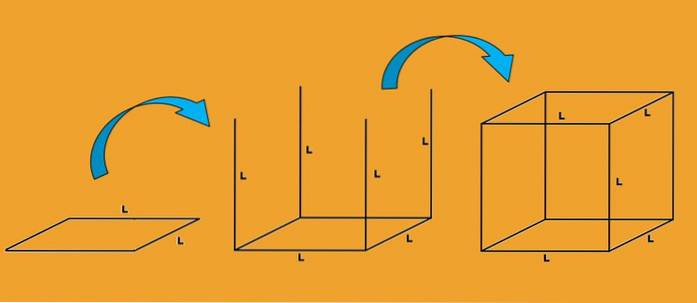
Dann werden vier vertikale Linien von jedem Scheitelpunkt gezogen, und die Länge jeder dieser Linien ist L. Jede Linie ist auch eine Kante des Würfels.

Schließlich wird ein weiteres Quadrat mit der Seite L gezeichnet, so dass seine Eckpunkte mit dem Ende der im vorherigen Schritt gezeichneten Kanten zusammenfallen. Jede der Seiten dieses neuen Quadrats ist eine Kante des Würfels.

3- Zauberwürfel

Um die geometrische Definition zu veranschaulichen, die zu Beginn angegeben wurde, können Sie sich einen Zauberwürfel ansehen.

Jedes Gesicht hat eine andere Farbe. Die Kanten werden durch die Linie dargestellt, an der sich die Flächen mit unterschiedlichen Farben schneiden.

Eulers Satz

Eulers Theorem für Polyeder besagt, dass bei einem Polyeder die Anzahl der Flächen C plus die Anzahl der Eckpunkte V gleich der Anzahl der Kanten A plus 2 ist. Das heißt, C + V = A + 2.

In den vorherigen Bildern sehen Sie, dass ein Würfel 6 Flächen, 8 Eckpunkte und 12 Kanten hat. Daher erfüllt es den Satz von Euler für Polyeder, da 6 + 8 = 12 + 2.

Es ist sehr nützlich, die Länge einer Würfelkante zu kennen. Wenn die Länge einer Kante bekannt ist, ist die Länge aller ihrer Kanten bekannt, mit denen bestimmte Daten des Würfels erhalten werden können, wie z. B. sein Volumen.

Das Volumen eines Würfels ist definiert als L³, wobei L die Länge seiner Kanten ist. Um das Volumen des Würfels zu kennen, muss daher nur der Wert von L bekannt sein.

Verweise

1. Guibert, A., Lebeaume, J. & Mousset, R. (1993). Geometrische Aktivitäten für die Säuglings- und Grundschulbildung: für die Säuglings- und Grundschulbildung. Narcea Editions.
2. Itzcovich, H. (2002). Das Studium von Figuren und geometrischen Körpern: Aktivitäten für die ersten Schuljahre. Noveduc Bücher.
3. Rendon, A. (2004). AKTIVITÄTEN NOTEBOOK 3 2. HOCHSCHULE. Editorial Tebar.
4. Schmidt, R. (1993). Beschreibende Geometrie mit stereoskopischen Figuren. Reverte.
5. Spectrum (Hrsg.). (2013). Geometrie, Klasse 5. Carson-Dellosa Publishing.