
Restitutionskoeffizient Konzept, Formel, Berechnung, Beispiel

Das Rückerstattungskoeffizient ist der Quotient zwischen der relativen Rückzugsgeschwindigkeit und der relativen Annäherungsgeschwindigkeit zweier kollidierender Körper. Wenn die Körper nach der Kollision vereint sind, ist dieser Quotient Null. Und das Gerät ist für den Fall wert, dass die Kollision perfekt elastisch ist.
Angenommen, zwei feste Massenkugeln M1 und Masse M2 jeweils die eine Kollision erleiden. Kurz vor der Kollision hatten die Kugeln Geschwindigkeiten V1 Y. V2 in Bezug auf ein bestimmtes Trägheitsreferenzsystem. Gleich nach der Kollision ändern sich ihre Geschwindigkeiten auf V1 ' Y. V2 '.
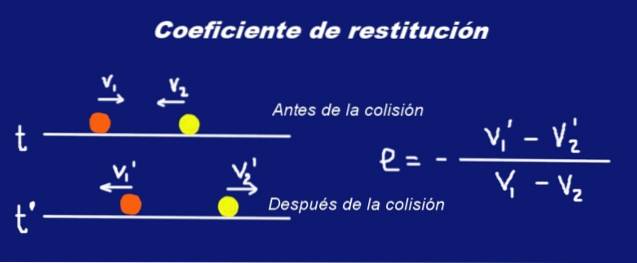
Brief wurde platziert fettgedruckte Schriftart in den Geschwindigkeiten, um anzuzeigen, dass es sich um Vektorgrößen handelt.
Experimente zeigen, dass jede Kollision die folgende Beziehung erfüllt:
V1 ' - V2 '= -und (V1 - V2)
Wo und ist eine reelle Zahl zwischen 0 und 1, die als bezeichnet wird Rückerstattungskoeffizient der Kollision. Der obige Ausdruck wird folgendermaßen interpretiert:
Die Relativgeschwindigkeit zweier Partikel vor der Kollision ist proportional zur Relativgeschwindigkeit der beiden Partikel nach der Kollision, die Proportionalitätskonstante ist (-e), wobei e der Restitutionskoeffizient der Kollision ist.
Artikelverzeichnis
- 1 Wofür ist der Rückerstattungskoeffizient??
- 1.1 Der Schwung
- 1.2 Energie und Rückerstattungskoeffizient
- 2 Wie berechnet sich der Restitutionskoeffizient??
- 3 Beispiel
- 3.1 Lösung
- 4 Referenzen
Wofür ist der Rückerstattungskoeffizient??
Die Nützlichkeit dieses Koeffizienten liegt in der Kenntnis des Grad der Unelastizität einer Kollision. In dem Fall, dass die Kollision vollkommen elastisch ist, ist der Koeffizient 1, während bei einer vollständig unelastischen Kollision der Koeffizient 0 ist, da in diesem Fall die relative Geschwindigkeit nach der Kollision Null ist..
Wenn umgekehrt der Restitutionskoeffizient einer Kollision und die Geschwindigkeiten der Partikel vor dieser bekannt sind, können die Geschwindigkeiten nach dem Auftreten der Kollision vorhergesagt werden..
Schwung
Bei Kollisionen gibt es neben der Beziehung, die den Restitutionskoeffizienten festlegt, eine weitere grundlegende Beziehung, nämlich die Impulserhaltung.
Schwung p eines Teilchens oder Impulses, wie er auch genannt wird, ist das Produkt der Masse M. des Teilchens durch seine Geschwindigkeit V.. Das heißt: die Dynamik p ist eine Vektorgröße.
Bei Kollisionen der lineare Impuls P. des Systems ist kurz vor und kurz nach der Kollision gleich, da die äußeren Kräfte im Vergleich zu den kurzen, aber intensiven Kräften der inneren Wechselwirkung während der Kollision vernachlässigbar sind. Die Erhaltung der Dynamik reicht jedoch nicht aus P. des Systems zur Lösung des allgemeinen Kollisionsproblems.
In dem zuvor erwähnten Fall, dem der beiden kollidierenden Massenkugeln M1 und M2, wird die Erhaltung des linearen Impulses wie folgt geschrieben:
M1 V1 + M2 V2 = M1 V1 ' + M2 V2 ' .
Es gibt keine Möglichkeit, das Kollisionsproblem zu lösen, wenn der Restitutionskoeffizient nicht bekannt ist. Die Impulserhaltung ist zwar notwendig, reicht jedoch nicht aus, um die Geschwindigkeit nach der Kollision vorherzusagen.
Wenn ein Problem besagt, dass die Körper nach der Kollision zusammen bleiben, heißt es implizit, dass der Restitutionskoeffizient 0 ist.

Energie und Rückerstattungskoeffizient
Die andere wichtige physikalische Größe bei Kollisionen ist Energie. Bei Kollisionen findet ein Austausch von kinetischer Energie, potentieller Energie und anderen Energiearten wie Wärmeenergie statt.
Vor und nach der Kollision ist die potentielle Wechselwirkungsenergie praktisch Null, sodass die Energiebilanz die kinetische Energie der Partikel vor und nach und eine Größe umfasst Q. dissipierte Energie genannt.
Für die beiden kollidierenden Massenkugeln M1 und M2 wird die Energiebilanz vor und nach der Kollision wie folgt geschrieben:
½ M1 V1^ 2 + ½ M2 V2^ 2 = ½ M1 V1 '^ 2 + ½ M2 V2 '^ 2 + Q.
Wenn die Wechselwirkungskräfte während der Kollision rein konservativ sind, kommt es vor, dass die gesamte kinetische Energie der kollidierenden Teilchen bleibt erhalten, dh es ist vor und nach der Kollision gleich (Q = 0). In diesem Fall gilt die Kollision als perfekt elastisch..
Bei elastischen Kollisionen wird keine Energie abgeführt. Darüber hinaus entspricht der Rückerstattungskoeffizient: e = 1.
Im Gegensatz dazu ist bei den unelastischen Kollisionen Q ≠ 0 und 0 ≤ e < 1. Sabemos, por ejemplo, que la colisión de las bolas de billar no es perfectamente elástica porque el sonido que se emite durante el impacto es parte de la energía disipada.
Damit ein Kollisionsproblem perfekt bestimmt werden kann, muss der Restitutionskoeffizient oder alternativ die während der Kollision verbrauchte Energiemenge bekannt sein.
Der Restitutionskoeffizient hängt von der Art und Art der Wechselwirkung zwischen den beiden Körpern während der Kollision ab..
Die Relativgeschwindigkeit der Körper vor der Kollision bestimmt ihrerseits die Intensität der Wechselwirkung und damit ihren Einfluss auf den Restitutionskoeffizienten..
Wie berechnet sich der Restitutionskoeffizient??
Um zu veranschaulichen, wie der Restitutionskoeffizient einer Kollision berechnet wird, nehmen wir einen einfachen Fall:
Angenommen, die Kollision zweier Massenkugeln M1 = 1 kg Y. M2 = 2 kg Bewegung auf einer geraden Schiene ohne Reibung (wie in Abbildung 1).
Die erste Kugel trifft mit Anfangsgeschwindigkeit V1 = 1 m / s auf der zweiten, die ursprünglich in Ruhe ist, das heißt V2 = 0 m / s.
Nach der Kollision bewegen sie sich weiter: Der erste stoppt (V1 '= 0 m / s) und der zweite bewegt sich mit Geschwindigkeit nach rechts V2 '= 1/2 m / s.
Um den Restitutionskoeffizienten bei dieser Kollision zu berechnen, wenden wir die Beziehung an:
V1 ' - V2 ' = -und (( V1 - V2 )
0 m / s - 1/2 m / s = - e (1 m / s - 0 m / s) => - 1/2 = - e => e = 1/2 .
Beispiel
Bei der eindimensionalen Kollision der beiden Kugeln des vorherigen Abschnitts wurde ihr Restitutionskoeffizient berechnet, was zu e = ½ führte .
Da e ≠ 1 die Kollision nicht elastisch ist, dh die kinetische Energie des Systems nicht erhalten bleibt und eine bestimmte Menge an Verlustleistung Q vorhanden ist (z. B. Erwärmung der Kugeln aufgrund der Kollision).
Bestimmen Sie den Wert der in Joule verbrauchten Energie. Berechnen Sie auch den prozentualen Anteil der verbrauchten Energie.
Lösung
Die anfängliche kinetische Energie von Kugel 1 ist:
K1i = ½ M1 V1 ^ 2 = ½ 1 kg (1 m / s) ^ 2 = ½ J.
während die der Kugel 2 Null ist, weil sie anfänglich in Ruhe ist.
Dann ist die anfängliche kinetische Energie des Systems Ki = ½ J..
Nach der Kollision bewegt sich nur die zweite Kugel mit der Geschwindigkeit V2 '= ½ m / s, sodass die endgültige kinetische Energie des Systems wie folgt lautet:
Kf = ½ M2 V2 '^ 2 = ½ 2 kg (½ m / s) ^ 2 = ¼ J.
Das heißt, die bei der Kollision verbrauchte Energie ist:
Q = Ki - Kf = (½ J - ¼ J) = 1/4 J.
Der Anteil der bei dieser Kollision verbrauchten Energie wird wie folgt berechnet:
f = Q / Ki = ¼ / ½ = 0,5, dh 50% der Energie des Systems wurden aufgrund der unelastischen Kollision mit einem Restitutionskoeffizienten von 0,5 verbraucht.
Verweise
- Bauer, W. 2011. Physik für Ingenieurwissenschaften. Band 1. Mc Graw Hill.
- Figueroa, D. 2005. Reihe: Physik für Naturwissenschaften und Technik. Band 1. Kinematik. Herausgegeben von Douglas Figueroa (USB).
- Knight, R. 2017. Physik für Wissenschaftler und Ingenieure: ein strategischer Ansatz. Pearson.
- Sears, Zemansky. 2016. Universitätsphysik mit moderner Physik. 14 .. Ed. Band 1.
- Wikipedia. Bewegungsumfang Wiederhergestellt von: en.wikipedia.org.



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.