
Wechselstromkreistypen, Anwendungen, Beispiele
Das Wechselstromkreise oder Wechselstromkreise bestehen aus Kombinationen von resistiven, induktiven und kapazitiven Elementen, kombiniert mit einer Wechselspannungsquelle, die normalerweise sinusförmig ist.
Durch Anlegen der Spannung wird für kurze Zeit ein variabler Strom aufgebaut, der als Übergangsstrom bezeichnet wird und dem sinusförmigen Stehstrom Platz macht.
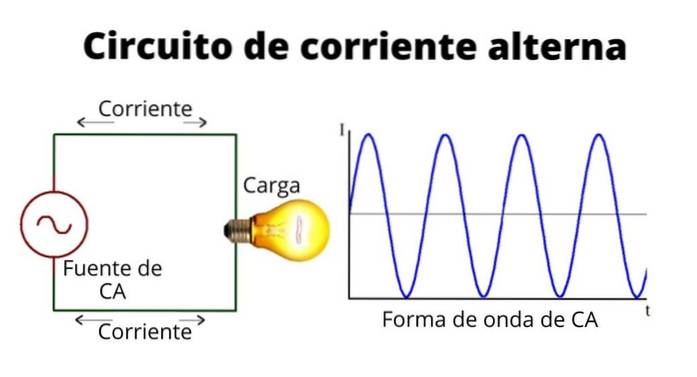
Der sinusförmige Strom hat Werte, die zwischen positiv und negativ wechseln und sich in regelmäßigen Abständen ändern, die durch eine zuvor festgelegte Frequenz bestimmt werden. Die Form des Stroms wird ausgedrückt als:
I (t) = I.m sin (ωt - φ)
Wo ichm ist der maximale Strom oder die maximale Stromamplitude, ω ist die Frequenz, t ist die Zeit und φ die Phasendifferenz. Häufig verwendete Stromeinheiten sind das Ampere (A) und seine Submultiplikatoren wie Milliampere und Mikroampere..
Die Zeit wird ihrerseits in Sekunden gemessen, für die Frequenz gibt es Hertz oder Hertz, abgekürzt Hz, während die Phasendifferenz ein Winkel ist, der im Allgemeinen im Bogenmaß gemessen wird, obwohl er manchmal auch in Grad angegeben wird. Weder diese noch das Bogenmaß werden als Einheiten betrachtet.

Oft wird die Wechselspannung durch die Welle innerhalb des Kreises symbolisiert, um sie von der Gleichspannung zu unterscheiden, die durch die beiden ungleichen und parallelen Linien symbolisiert wird.
Artikelverzeichnis
- 1 Arten von Wechselstromkreisen
- 1.1 Schaltung mit Widerstandselement
- 1.2 Schaltung mit induktivem Element
- 1.3 Schaltung mit kapazitivem Element
- 2 Anwendungen
- 2.1 Phasenschaltkreise
- 2.2 Brückenschaltungen
- 3 Beispiele für Wechselstromkreise
- 3.1 Beispiel 1: Serien-RLC-Schaltung
- 3.2 Beispiel 2: RLC-Schaltung parallel
- 4 Übung gelöst
- 4.1 Lösung a
- 4.2 Lösung b
- 4.3 Lösung c
- 5 Themen von Interesse
- 6 Referenzen
Arten von Wechselstromkreisen
Es gibt viele Arten von Wechselstromkreisen, beginnend mit den einfachsten in der folgenden Abbildung gezeigten Stromkreisen. Von links nach rechts haben Sie:
-Schaltung mit Widerstand R.
-Schaltung mit Spule L.
-Schaltung mit Kondensator C..

Schaltung mit Widerstandselement
In der Schaltung mit einem Widerstand R, der an eine Wechselspannungsquelle angeschlossen ist, beträgt die Spannung über dem Widerstand V.R. = V.m sen ωt. Nach dem Ohmschen Gesetz, das auch für rein ohmsche Wechselstromkreise gilt:
V.R. = IchR.∙ R.
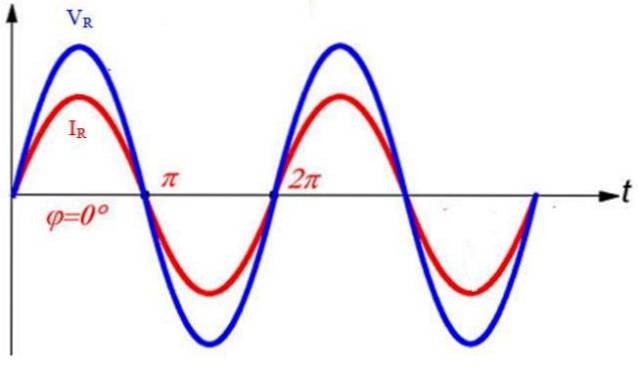
Daher ist der maximale Strom I.m = V.m / R..
Sowohl Strom als auch Spannung sind in Phase, was bedeutet, dass sie gleichzeitig ihre Maximalwerte sowie 0 erreichen.

Induktive Elementschaltung
In der Spule L beträgt die Spannung V.L. = V.m sin ωt und hängt mit dem Strom in der Induktivität durch die folgende Gleichung zusammen:
Integrieren:

Durch Eigenschaften von trigonometrischen Verhältnissen, I.L. wird in Form von sin ωt geschrieben als:
ichL. = Ichm sin (ωt - ½ π)
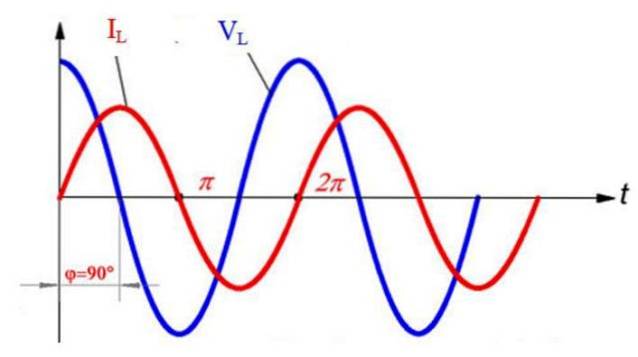
Dann sind die Spannung und der Strom phasenverschoben, wobei letzteres in Bezug auf die Spannung ½ π = 90º nacheilt (der Strom beginnt früher, wobei t = 0 s der Startpunkt ist). Dies ist in der folgenden Abbildung zu sehen, die die Sinuskurve von I vergleichtL. und das von V.L.::

Induktive Reaktanz
Die induktive Reaktanz ist als X definiertL. = ωL, nimmt mit der Frequenz zu und hat Widerstandsdimensionen, daher in Analogie zum Ohmschen Gesetz:
V.L. = IchL. ∙ X.L.
Schaltung mit kapazitivem Element
Für einen Kondensator C, der an eine Wechselstromquelle angeschlossen ist, gilt Folgendes:
Q = C ∙ V.C. = C ∙ V.m sen ωt
Der Strom im Kondensator wird durch zeitliche Verschiebung der Ladung ermittelt:
ichC.= ωC ∙ V.m cos ωt
Aber cos ωt = sin (ωt + ½ π), dann:
ichC. = ωCVm sin (ωt + ½ π)
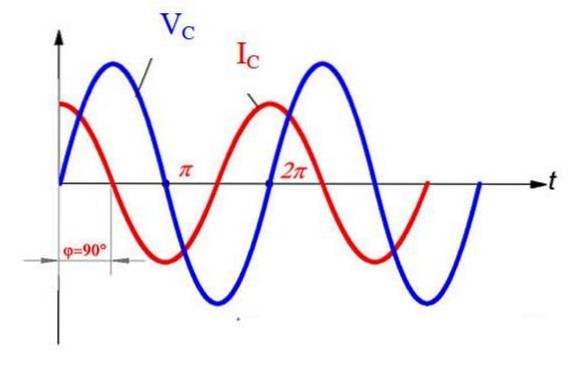
In diesem Fall liegt der Strom um ½ π vor der Spannung, wie aus dem Diagramm ersichtlich ist.

Kapazitive Reaktanz
Kapazitive Reaktanz kann X geschrieben werdenC. = 1 / ωC, nimmt mit der Frequenz ab und hat auch Widerstandseinheiten, dh Ohm. Auf diese Weise sieht das Ohmsche Gesetz folgendermaßen aus:
V.C. = X.C..ichC.
Anwendungen
Michael Faraday (1791-1867) war der erste, der durch seine Induktionsexperimente einen Strom erhielt, der seine Bedeutung periodisch änderte, obwohl in den frühen Tagen nur Gleichstrom verwendet wurde..
Ende des 19. Jahrhunderts kam es zwischen Thomas A. Edison, Verteidiger der Gleichstromnutzung, und George Westinghouse, Anhänger des Wechselstroms, zu dem bekannten Krieg der Strömungen. Schließlich war dies derjenige, der aufgrund der Wirtschaftlichkeit, Effizienz und einfachen Übertragung mit geringeren Verlusten gewann..
Aus diesem Grund ist der Strom, der bis heute in Haushalte und Industrie gelangt, Wechselstrom, obwohl die Verwendung von Gleichstrom nie vollständig verschwunden ist..
Wechselstrom wird für fast alles verwendet, und in vielen Anwendungen ist die ständige Richtungsänderung des Wechselstroms nicht relevant, wie z. B. Glühbirnen, Bügeleisen oder Herd zum Kochen, da die Erwärmung des Widerstandselements nicht von der abhängt Bewegungsrichtung der Lasten.
Stattdessen ist die Tatsache, dass der Strom mit einer bestimmten Frequenz die Richtung ändert, die Grundlage für Elektromotoren und verschiedene spezifischere Anwendungen, wie zum Beispiel die folgenden:
Phasenverschiebungsschaltungen
Schaltungen, die aus einer Wechselquelle bestehen, die mit einem Widerstand und einem Kondensator in Reihe geschaltet ist, werden als RC-Reihenschaltungen bezeichnet und dienen dazu, unerwünschte Phasenverschiebungen in einer anderen Schaltung zu beseitigen oder ihr einen besonderen Effekt zu verleihen..
Sie dienen auch als Spannungsteiler und zum Einstellen von Radiosendern (siehe Beispiel 1 im nächsten Abschnitt)..
Brückenschaltungen
Mit Wechselstrom gespeiste Brückenschaltungen können zur Messung der Kapazität oder Induktivität verwendet werden, genau wie die Wheatstone-Brücke, eine bekannte Gleichstromschaltung, die den Wert eines unbekannten Widerstands messen kann..
Beispiele für Wechselstromkreise
In den vorhergehenden Abschnitten wurden die einfachsten Wechselstromkreise beschrieben, obwohl natürlich die oben beschriebenen Grundelemente sowie andere etwas komplexere wie Dioden, Verstärker und Transistoren, um nur einige zu nennen, kombiniert werden können, um verschiedene Effekte zu erzielen ..
Beispiel 1: Serien-RLC-Schaltung
Eine der häufigsten Schaltungen in AC ist derjenige, der einen Widerstand R, eine Spule oder Induktivität L und einen Kondensator oder Kondensator C enthält, der in Reihe mit einer Wechselstromquelle geschaltet ist.
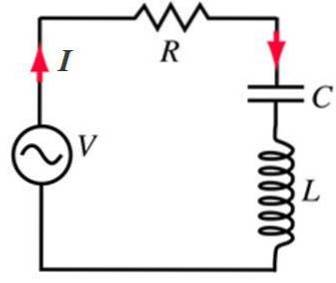
Serien-RLC-Schaltungen reagieren auf besondere Weise auf die Frequenz der Wechselquelle, von der sie gespeist werden. Aus diesem Grund ist eine der interessantesten Anwendungen die Verwendung von Radio-Tuner-Schaltkreisen..
Ein Funksignal mit der Frequenz ω erzeugt einen Strom mit derselben Frequenz in einer Schaltung, die speziell als Empfänger ausgelegt ist, und die Amplitude dieses Stroms ist maximal, wenn der Empfänger durch einen genannten Effekt auf diese Frequenz abgestimmt ist Resonanz.
Die Empfängerschaltung dient als Tuner, da sie so ausgelegt ist, dass Signale mit unerwünschten Frequenzen sehr kleine Ströme erzeugen, die von den Radiolautsprechern nicht erkannt werden und daher nicht hörbar sind. Stattdessen erreicht bei der Resonanzfrequenz die Amplitude des Stroms ein Maximum und dann ist das Signal deutlich zu hören..
Die Resonanzfrequenz tritt auf, wenn sich die induktiven und kapazitiven Reaktanzen der Schaltung ausgleichen:
X.L. = X.C.
1 / ωC = ωL
ωzwei = 1 / LC
Der Radiosender mit dem Frequenzsignal ω wird als "abgestimmt" bezeichnet, und die Werte von L und C werden für diese bestimmte Frequenz ausgewählt..
Beispiel 2: RLC-Schaltung parallel
Parallele RLC-Schaltungen haben auch bestimmte Reaktionen entsprechend der Frequenz der Quelle, die von der Reaktanz jedes der Elemente abhängt, definiert als das Verhältnis zwischen Spannung und Strom..
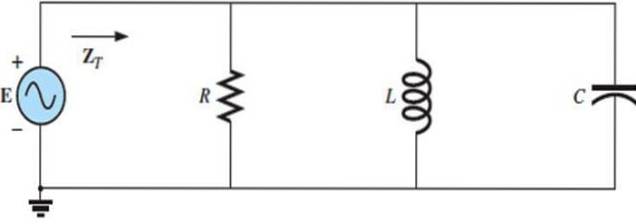
Übung gelöst
In der Serien-LRC-Schaltung von Beispiel 1 im vorhergehenden Abschnitt beträgt der Widerstand 200 Ohm, die Induktivität 0,4 H und der Kondensator 6 uF. Die Stromversorgung ist ihrerseits eine Wechselspannung mit einer Amplitude von 30 V und einer Frequenz von 250 rad / s. Es wird gebeten zu finden:
a) Die Reaktanzen jedes Elements
b) Der Wert des Moduls der Impedanz der Schaltung.
c) Die Amplitude des Stroms
Lösung für
Die jeweiligen Reaktanzen werden mit den Formeln berechnet:
X.C. = 1 / & ohgr; C = 1 / (250 rad / s × 6 × 10-6 F) = 666,67 Ohm
X.L. = ωL = 250 rad / s x 0,4 H = 100 Ohm
Und die Reaktanz des Widerstands entspricht seinem Wert in Ohm:
X.R. = R = 200 Ohm
Lösung b
Die Impedanz Z ist definiert als das Verhältnis von Spannung zu Strom in der Schaltung, entweder in Reihe oder parallel:
Z = V.m / ICHm
Die Impedanz wird in Ohm gemessen, genau wie ein Widerstand oder eine Reaktanz, bezieht sich jedoch auf den Widerstand gegen den Stromdurchgang der Induktivitäten und Kondensatoren, wenn man bedenkt, dass zusätzlich zu ihren besonderen Effekten, wie z. B. Verzögerung oder Vorschub der Spannung, es hat auch einen gewissen Innenwiderstand.
Es kann gezeigt werden, dass für die Serien-RLC-Schaltung der Impedanzmodul gegeben ist durch:
Bei der Bewertung der in der Anweisung angegebenen Werte erhalten wir:

Lösung c
Von:
Z = V.m / ICHm
Es muss;
ichm = V.m / Z = 30 V / 601 Ohm = 0,05 A..
Themen von Interesse
Unterschiede zwischen Wechsel- und Gleichstrom
Verweise
- Alexander, C. 2006. Grundlagen elektrischer Schaltungen. 3 .. Auflage. Mc Graw Hill.
- Boylestad, R. 2011. Einführung in die Schaltungsanalyse.2da. Auflage. Pearson.
- Figueroa, D. (2005). Reihe: Physik für Wissenschaft und Technik. Band 6. Elektromagnetismus. Herausgegeben von Douglas Figueroa (USB).
- Sears, Zemansky. 2016. Universitätsphysik mit moderner Physik. 14 .. Ed. Band 1. Pearson.
- Serway, R., Jewett, J. (2008). Physik für Wissenschaft und Technik. Band 1. 7 .. Ed. Lernen einbinden.


Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.