
Carnot-Zyklusphasen, Anwendungen, Beispiele, Übungen
Das Carnot-Zyklus Es ist die Abfolge von thermodynamischen Prozessen, die in einem Carnot-Motor stattfinden, einem idealen Gerät, das nur aus Prozessen vom reversiblen Typ besteht. das heißt, diejenigen, die stattgefunden haben, können in den Ausgangszustand zurückkehren.
Dieser Motortyp wird als ideal angesehen, da ihm die in realen Maschinen auftretende Verlustleistung, Reibung oder Viskosität fehlt, wodurch Wärmeenergie in nutzbare Arbeit umgewandelt wird, obwohl die Umwandlung nicht zu 100% erfolgt.

Ein Motor wird ausgehend von einer arbeitsfähigen Substanz wie Gas, Benzin oder Dampf gebaut. Diese Substanz ist verschiedenen Temperaturänderungen ausgesetzt und erfährt wiederum Schwankungen in Druck und Volumen. Auf diese Weise ist es möglich, einen Kolben innerhalb eines Zylinders zu bewegen.
Artikelverzeichnis
- 1 Was ist der Carnot-Zyklus??
- 2 Stufen des Carnot-Zyklus
- 2.1 Ausgangspunkt
- 2.2 Erste Stufe: isotherme Expansion
- 2.3 Zweite Stufe: adiabatische Expansion
- 2.4 Dritte Stufe: isotherme Kompression
- 2.5 Vierte Stufe: adiabatische Kompression
- 3 Carnots Satz
- 3.1 Beweis des Satzes von Carnot
- 3.2 Folgerung aus Satz und Grenzen
- 4 Beispiele
- 4.1 Ein Kolben in einem Zylinder
- 4.2 Verschiedene reversible Prozesse
- 4.3 Ein Kernkraftwerk
- 5 Übungen gelöst
- 5.1 - Beispiel 1: Wirkungsgrad einer Wärmekraftmaschine
- 5.2 - Beispiel 2: Wärmeaufnahme und Wärmeübertragung
- 6 Referenzen
Was ist der Carnot-Zyklus??
Der Carnot-Zyklus findet in einem System statt, das als Carnot-Motor oder C bezeichnet wird. Dies ist ein ideales Gas, das in einem Zylinder eingeschlossen und mit einem Kolben versehen ist, der mit zwei Quellen bei unterschiedlichen Temperaturen T in Kontakt steht1 und Tzwei wie in der Abbildung unten links gezeigt.
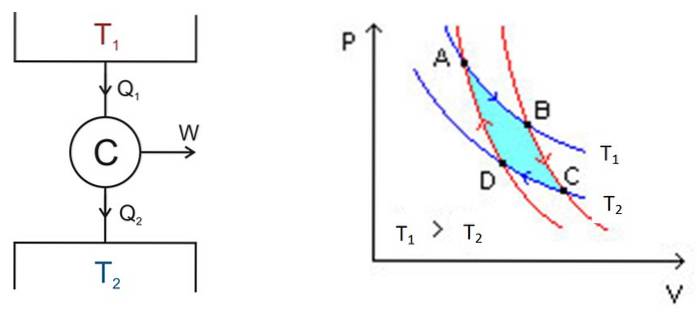
Dort finden folgende grobe Prozesse statt:
- Dem Gerät Q wird eine bestimmte Wärmemenge zugeführtEintrag = Q.1 aus dem Thermotank bei hoher Temperatur T.1.
- Carnots Motor C führt dank dieser zugeführten Wärme die Arbeit W aus.
- Ein Teil der verwendeten Wärme: der Abfall Q.Ausfahrt, wird in den Thermotank überführt, der eine niedrigere Temperatur T hatzwei.
Phasen des Carnot-Zyklus
Die Analyse wird unter Verwendung eines P-V-Diagramms (Druck-Volumen) durchgeführt, wie in Abbildung 2 (rechte Abbildung) gezeigt. Der Zweck des Motors kann darin bestehen, den Wärmespeicher 2 kühl zu halten und ihm Wärme zu entziehen. In diesem Fall ist es ein Kühlmaschine. Wenn Sie andererseits Wärme an den Wärmespeicher 1 übertragen möchten, ist dies a Wärmepumpe.
Das P-V-Diagramm zeigt die Änderungen von Druck und Temperatur des Motors unter zwei Bedingungen:
- Temperatur konstant halten (isothermer Prozess).
- Keine Wärmeübertragung (Wärmedämmung).
Die beiden isothermen Prozesse müssen miteinander verbunden werden, was durch Wärmedämmung erreicht wird.
Punkt
Sie können an jedem Punkt des Zyklus beginnen, an dem das Gas bestimmte Druck-, Volumen- und Temperaturbedingungen aufweist. Das Gas durchläuft eine Reihe von Prozessen und kann zu den Ausgangsbedingungen zurückkehren, um einen weiteren Zyklus zu starten. Die endgültige innere Energie ist immer dieselbe wie die ursprüngliche. Da Energie gespart wird:
Arbeit erledigt mit C = Wärmeeintrag - Wärmeeintrag
ΔW = Q.Eintrag - Q.Ausfahrt
Die Fläche innerhalb dieser Schleife oder Schleife, in der Abbildung türkis, entspricht genau der Arbeit des Carnot-Motors.
In Abbildung 2 sind die Punkte A, B, C und D markiert. Wir beginnen bei Punkt A und folgen dem blauen Pfeil..
Erste Stufe: isotherme Expansion
Die Temperatur zwischen den Punkten A und B beträgt T.1. Das System nimmt Wärme aus dem Wärmespeicher 1 auf und erfährt eine isotherme Expansion. Dann nimmt das Volumen zu und der Druck ab.
Die Temperatur bleibt jedoch bei T.1, denn wenn sich das Gas ausdehnt, kühlt es ab. Daher bleibt seine innere Energie konstant.
Zweite Stufe: adiabatische Expansion
Bei Punkt B beginnt das System eine neue Erweiterung, bei der das System weder Wärme gewinnt noch verliert. Dies wird erreicht, indem es wie oben angegeben in eine Wärmeisolierung eingebracht wird. Daher handelt es sich um eine adiabatische Erweiterung, die nach dem roten Pfeil weiter auf Punkt C zeigt. Das Volumen nimmt zu und der Druck sinkt auf den niedrigsten Wert.
Dritte Stufe: isotherme Kompression
Sie beginnt am Punkt C und endet am D. Die Isolierung wird entfernt und das System kommt mit dem Thermotank 2 in Kontakt, dessen Temperatur T.zwei ist weniger. Das System überträgt Abwärme an den Wärmespeicher, der Druck steigt an und das Volumen nimmt ab.
Vierte Stufe: adiabatische Kompression
Am Punkt D kehrt das System zur Wärmedämmung zurück, der Druck steigt und das Volumen nimmt ab, bis es die ursprünglichen Bedingungen von Punkt A erreicht. Dann wiederholt sich der Zyklus erneut..
Carnots Satz
Carnots Satz wurde erstmals im frühen 19. Jahrhundert vom französischen Physiker Sadi Carnot postuliert. 1824 veröffentlichte Carnot, der Teil der französischen Armee war, ein Buch, in dem er die Antwort auf die folgende Frage vorschlug: Unter welchen Bedingungen hat eine Wärmekraftmaschine einen maximalen Wirkungsgrad? Carnot stellte dann Folgendes fest:
Keine Wärmekraftmaschine, die zwischen zwei Wärmespeichern läuft, ist effizienter als die Carnot-Maschine.
Der Wirkungsgrad η einer Wärmekraftmaschine ergibt sich aus dem Quotienten zwischen der geleisteten Arbeit W und der aufgenommenen Wärme Q:
Leistung = geleistete Arbeit / aufgenommene Wärme
Auf diese Weise ist der Wirkungsgrad jeder Wärmekraftmaschine I: η = W / Q. Während der Wirkungsgrad eines Carnot-Motors R η '= W / Q' ist, wird angenommen, dass beide Motoren die gleiche Arbeit leisten können.
Carnots Satz besagt, dass η niemals größer als η 'ist. Andernfalls widerspricht es dem zweiten Hauptsatz der Thermodynamik, wonach ein Prozess, bei dem Wärme aus einem Körper mit niedrigerer Temperatur austritt, um auf eine höhere Temperatur zu gelangen, ohne externe Hilfe zu erhalten, unmöglich ist. Deshalb:
η < η'
Beweis von Carnots Satz
Um dies zu zeigen, betrachten Sie den Carnot-Motor als eine Kühlmaschine, die von einem I-Motor angetrieben wird. Dies ist möglich, da der Carnot-Motor wie zu Beginn angegeben durch reversible Prozesse arbeitet..
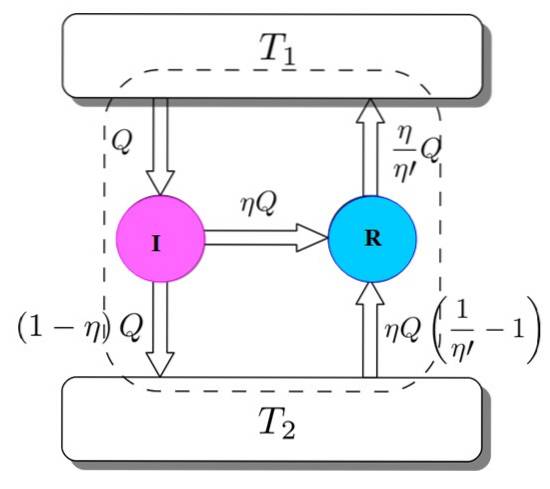
Wir haben beide: I und R arbeiten mit denselben Wärmespeichern und es wird angenommen, dass η > η'. Wenn auf dem Weg ein Widerspruch zum zweiten Hauptsatz der Thermodynamik erreicht wird, wird Carnots Satz durch Reduktion auf die Absurdität bewiesen.
Abbildung 3 hilft Ihnen dabei, den Prozess zu verfolgen. Der Motor I nimmt eine Wärmemenge Q auf, die er auf folgende Weise aufteilt: Er arbeitet an R, das W = ηQ entspricht, und der Rest ist die Wärme, die (1-η) Q an den Wärmespeicher T übertragen wirdzwei.
Da Energie gespart wird, sind alle folgenden Aussagen zutreffend:
UNDEintrag = Q = Arbeit W + Wärme, die an T abgegeben wirdzwei = ηQ + (1-η) Q = E.Ausfahrt
Nun entnimmt die Carnot-Kältemaschine R dem Wärmespeicher 2 eine Wärmemenge, die gegeben ist durch:
(η / η ') (1-η') Q =
Auch in diesem Fall muss Energie gespart werden:
UNDEintrag = ηQ + (η / η ') (1-η') Q = (η / η ') Q = Q' = E.Ausfahrt
Das Ergebnis ist die Übertragung in den Thermotank T.zwei einer Wärmemenge gegeben durch (η / η ') Q = Q'.
Wenn η größer als η 'ist, bedeutet dies, dass mehr Wärme die thermische Ablagerung mit höherer Temperatur erreicht hat, als ich ursprünglich angenommen habe. Da kein externes Mittel wie eine andere Wärmequelle beteiligt war, kann nur der kälteste Wärmespeicher die Wärme abgeben..
Dies steht im Widerspruch zum zweiten Hauptsatz der Thermodynamik. Daraus wird geschlossen, dass es nicht möglich ist, dass η' ist kleiner als η, daher kann der Motor I nicht effizienter sein als die Carnot-Maschine R..
Folgerung aus Satz und Grenzen
Die Konsequenz aus dem Satz von Carnot besagt, dass zwei Carnot-Maschinen den gleichen Wirkungsgrad haben, wenn beide mit den gleichen Wärmespeichern arbeiten..
Das heißt, unabhängig von der Substanz ist die Leistung unabhängig und kann nicht durch Änderung gesteigert werden..
Die Schlussfolgerung aus der obigen Analyse ist, dass der Carnot-Zyklus die ideal erreichbare Spitze des thermodynamischen Prozesses ist. In der Praxis gibt es viele Faktoren, die die Effizienz verringern, zum Beispiel die Tatsache, dass die Isolierung niemals perfekt ist und in den adiabatischen Stadien tatsächlich ein Wärmeaustausch mit der Außenseite stattfindet.
Bei einem Auto wird der Motorblock heiß. Andererseits verhält sich das Gemisch aus Benzin und Luft nicht genau wie ein ideales Gas, das der Ausgangspunkt des Carnot-Zyklus ist. Dies sind nur einige Faktoren, die zu einer drastischen Leistungsminderung führen.
Beispiele
Ein Kolben in einem Zylinder
Wenn das System ein Kolben ist, der wie in Abbildung 4 in einem Zylinder eingeschlossen ist, steigt der Kolben während der isothermen Expansion an, wie im ersten Diagramm ganz links zu sehen ist, und steigt auch während der adiabatischen Expansion an.
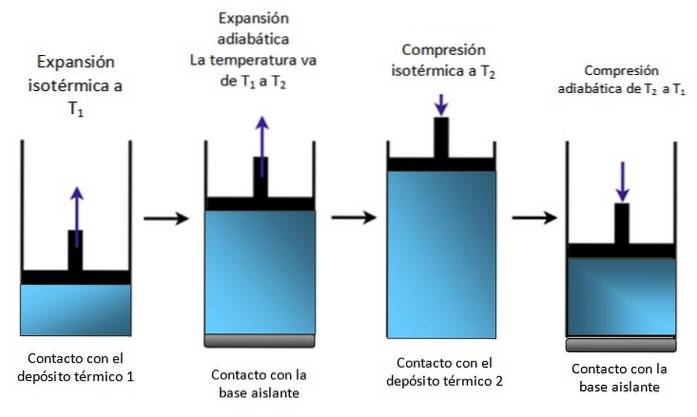
Es wird dann isotherm komprimiert, gibt Wärme ab und komprimiert weiter adiabatisch. Das Ergebnis ist eine Bewegung, bei der der Kolben im Zylinder auf und ab geht und die auf andere Teile einer bestimmten Vorrichtung übertragen werden kann, beispielsweise auf einen Automotor, der ein Drehmoment erzeugt, oder eine Dampfmaschine.
Verschiedene reversible Prozesse
Neben der Expansion und Kompression eines idealen Gases in einem Zylinder gibt es andere ideale reversible Prozesse, mit denen ein Carnot-Zyklus konfiguriert werden kann, zum Beispiel:
- Hin- und Herbewegungen ohne Reibung.
- Eine ideale Feder, die komprimiert und dekomprimiert und sich niemals verformt.
- Stromkreise, in denen es keine Widerstände gibt, um Energie abzuleiten.
- Magnetisierungs- und Entmagnetisierungszyklen, bei denen keine Verluste auftreten.
- Laden und Entladen eines Akkus.
Ein Kernkraftwerk
Obwohl es sich um ein sehr komplexes System handelt, ist eine erste Annäherung an das, was zur Energieerzeugung in einem Kernreaktor erforderlich ist, wie folgt:
- Eine Wärmequelle, die aus einem radioaktiv zerfallenden Material wie Uran besteht.
- Der kalte Kühlkörper oder Speicher, der die Atmosphäre wäre.
- Der "Carnot-Motor", der eine Flüssigkeit verwendet, fast immer Leitungswasser, dem Wärme von der Wärmequelle zugeführt wird, um sie in Dampf umzuwandeln.
Wenn der Zyklus ausgeführt wird, wird elektrische Energie als Netz gewonnen. Wenn das Wasser bei hoher Temperatur in Dampf umgewandelt wird, erreicht es eine Turbine, in der die Energie in Bewegung oder kinetische Energie umgewandelt wird.
Die Turbine wiederum treibt einen elektrischen Generator an, der die Energie seiner Bewegung in elektrische Energie umwandelt. Neben spaltbarem Material wie Uran können natürlich auch fossile Brennstoffe als Wärmequelle eingesetzt werden..
Gelöste Übungen
-Beispiel 1: Wirkungsgrad einer Wärmekraftmaschine
Der Wirkungsgrad einer Wärmekraftmaschine ist definiert als der Quotient zwischen der Ausgangsarbeit und der Eingangsarbeit und daher eine dimensionslose Größe:
Maximaler Wirkungsgrad = (Q.Eintrag - Q. Ausfahrt) / Q.Eintrag
Bezeichnet die maximale Effizienz als emax, Es ist möglich, seine Abhängigkeit von der Temperatur zu demonstrieren, die die am einfachsten zu messende Variable ist, wie zum Beispiel:
undmax = 1 - (T.zwei/ T.1)
Wo T.zwei ist die Sumpftemperatur und T.1 ist die Temperatur der Wärmequelle. Da letzteres größer ist, stellt sich heraus, dass der Wirkungsgrad immer kleiner als 1 ist.
Angenommen, Sie haben eine Wärmekraftmaschine, die auf folgende Weise betrieben werden kann: a) Zwischen 200 K und 400 K, b) Zwischen 600 K und 400 K. Wie hoch ist jeweils der Wirkungsgrad??
Lösung
a) Im ersten Fall beträgt die Effizienz:
undmax1 = 1 - (200/400) = 0,50
b) Für den zweiten Modus beträgt der Wirkungsgrad:
undmax2 = 1- (400/600) = 0,33
Obwohl der Temperaturunterschied zwischen beiden Modi gleich ist, ist der Wirkungsgrad nicht gleich. Noch bemerkenswerter ist, dass der effizienteste Modus bei einer niedrigeren Temperatur arbeitet..
-Beispiel 2: Wärmeaufnahme und Wärmeabgabe
Eine 22% effiziente Wärmekraftmaschine produziert 1.530 J Arbeit. Finden Sie: a) Die Wärmemenge, die vom Wärmespeicher 1 absorbiert wird, b) Die Wärmemenge, die an den Wärmespeicher 2 abgegeben wird.
a) In diesem Fall wird die Definition des Wirkungsgrads verwendet, da die durchgeführten Arbeiten verfügbar sind, nicht die Temperaturen der Wärmetanks. Ein Wirkungsgrad von 22% bedeutet, dass e max = 0,22, daher:
Maximale Effizienz = Arbeit / Q.Eintrag
Die aufgenommene Wärmemenge ist genau Q.Eintrag, so klar haben wir:
Q.Eintrag = Arbeit / Effizienz = 1530 J / 0,22 = 6954,5 J.
b) Die auf den kältesten Tank übertragene Wärmemenge ergibt sich aus ΔW = Q.Eintrag - Q.Ausfahrt
Q.Ausfahrt = Q.Eintrag - ΔW = 6954,5-1530 J = 5424,5 J..
Ein anderer Weg ist von undmax = 1 - (T.zwei/ T.1). Da die Temperaturen nicht bekannt sind, aber mit der Wärme zusammenhängen, kann der Wirkungsgrad auch ausgedrückt werden als:
undmax = 1 - (Q.gab nach/ Q.absorbiert)
Verweise
- Bauer, W. 2011. Physik für Ingenieurwissenschaften. Band 1. Mc Graw Hill. 654-657
- Kernenergie. Betrieb eines Kernkraftwerks. Wiederhergestellt von: energia-nuclear.net
- Serway, R., Jewett, J. (2008). Physik für Wissenschaft und Technik. Band 1. 7 .. Ed. Lernen einbinden. 618-622.
- Tippens, P. 2011. Physik: Konzepte und Anwendungen. 7. Auflage. MacGraw Hill. 414-416.
- Walker, J. 2008. Physik. 4. Aufl. Addison Wesley. 610-630



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.