Das Brayton-Zyklus ist ein thermodynamischer Zyklus, der aus vier Prozessen besteht und auf ein komprimierbares thermodynamisches Fluid wie ein Gas angewendet wird. Die erste Erwähnung stammt aus dem späten 18. Jahrhundert, obwohl es einige Zeit dauerte, bis sie von James Joule zum ersten Mal erwähnt wurde. Aus diesem Grund wird es auch als Joule-Zyklus bezeichnet..
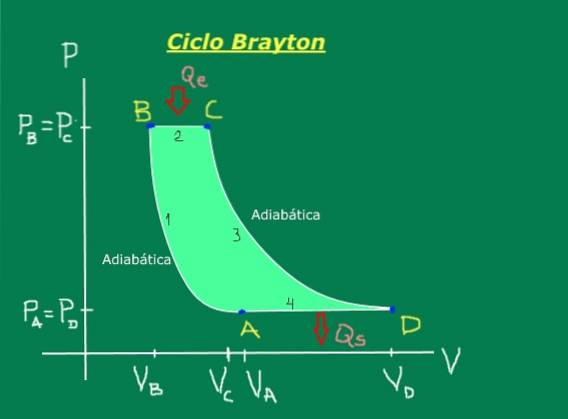
Es besteht aus den folgenden Stufen, die im Druck-Volumen-Diagramm in Abbildung 1 zweckmäßigerweise dargestellt sind: adiabatische Kompression (keine Wärme wird ausgetauscht), isobare Expansion (tritt bei konstantem Druck auf), adiabatische Expansion (keine Wärme wird ausgetauscht) und isobare Kompression (tritt bei konstantem Druck auf).
Artikelverzeichnis
Der Brayton-Zyklus ist der ideale thermodynamische Zyklus, der am besten angewendet wird, um den thermodynamischen Betrieb von Gasturbinen und Luft-Kraftstoff-Gemischen zu erklären, die zur Erzeugung elektrischer Energie und in Flugzeugtriebwerken verwendet werden.
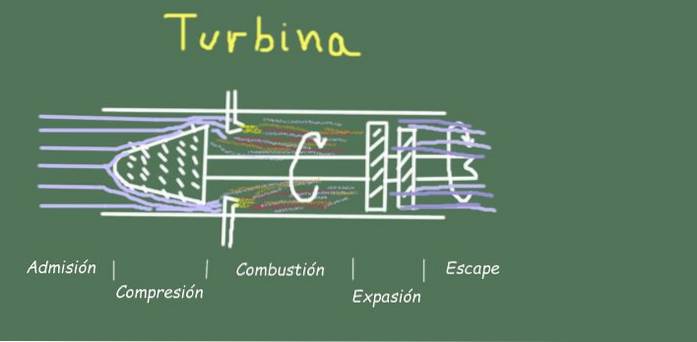
Zum Beispiel gibt es beim Betrieb einer Turbine mehrere Stufen im Betriebsgasstrom, die wir unten sehen werden.
Es besteht aus dem Einlass von Luft bei Umgebungstemperatur und -druck durch die Einlassöffnung der Turbine.
Luft wird durch Drehen der Schaufeln gegen feststehende Schaufeln im Kompressorabschnitt der Turbine komprimiert. Diese Kompression ist so schnell, dass praktisch kein Wärmeaustausch stattfindet, und wird daher durch den adiabatischen Prozess AB des Brayton-Zyklus modelliert. Die Luft am Kompressorausgang hat ihren Druck und ihre Temperatur erhöht.
Die Luft wird mit Propangas oder pulverisiertem Kraftstoff gemischt, der durch die Einspritzdüsen der Brennkammer eingeführt wird. Das Gemisch erzeugt eine chemische Verbrennungsreaktion.
Diese Reaktion liefert die Wärme, die die Temperatur und die kinetische Energie der Gaspartikel erhöht, die sich in der Brennkammer bei konstantem Druck ausdehnen. Im Brayton-Zyklus wird dieser Schritt mit dem BC-Prozess modelliert, der bei konstantem Druck abläuft.
Im Abschnitt der Turbine selbst dehnt sich die Luft weiter gegen die Turbinenschaufeln aus, wodurch sie sich dreht und mechanische Arbeit erzeugt. In diesem Schritt senkt die Luft ihre Temperatur, ohne jedoch praktisch Wärme mit der Umgebung auszutauschen..
Im Brayton-Zyklus wird dieser Schritt als adiabatischer CD-Expansionsprozess simuliert. Ein Teil der Arbeit der Turbine wird auf den Kompressor übertragen und der andere Teil wird zum Antrieb eines Generators oder Propellers verwendet.
Die ausströmende Luft hat einen konstanten Druck, der dem Umgebungsdruck entspricht, und überträgt Wärme an die enorme Masse der Außenluft, sodass sie in kurzer Zeit die gleiche Temperatur wie die Einlassluft annimmt. Im Brayton-Zyklus wird dieser Schritt mit dem DA-Prozess mit konstantem Druck simuliert, wodurch der thermodynamische Zyklus geschlossen wird.
Wir schlagen vor, die Effizienz des Brayton-Zyklus zu berechnen, für den wir von der Definition ausgehen.
In einer Wärmekraftmaschine ist der Wirkungsgrad definiert als das von der Maschine geleistete Netz geteilt durch die zugeführte Wärmeenergie.
Das erste Prinzip der Thermodynamik besagt, dass die Nettowärme, die in einem thermodynamischen Prozess zu einem Gas beiträgt, gleich der Änderung der inneren Energie des Gases zuzüglich der von ihm geleisteten Arbeit ist..
In einem vollständigen Zyklus ist die Variation der inneren Energie jedoch Null, sodass die im Zyklus eingebrachte Nettowärme gleich der geleisteten Nettoarbeit ist..
Der vorherige Ausdruck erlaubt es uns, den Wirkungsgrad als Funktion der absorbierten oder eingehenden Wärme Qe (positiv) und der übertragenen oder ausgehenden Wärme Qs (negativ) zu schreiben..
Im Brayton-Zyklus tritt Wärme in den isobaren Prozess BC ein und tritt im isobaren Prozess DA aus.
Unter der Annahme, dass n Mol Gas bei konstantem Druck im Prozess BC mit fühlbarer Wärme Qe versorgt werden, steigt seine Temperatur gemäß der folgenden Beziehung von Tb auf Tc:
Abgehende Wärme Qs kann auf ähnliche Weise durch die folgende Beziehung berechnet werden, die für den Konstantdruckprozess DA gilt:
Durch Einsetzen dieser Ausdrücke in den Ausdruck, der uns den Wirkungsgrad als Funktion der ein- und ausgehenden Wärme gibt, wobei die entsprechenden Vereinfachungen vorgenommen werden, wird die folgende Beziehung für den Wirkungsgrad erhalten:
Es ist möglich, das vorherige Ergebnis zu vereinfachen, wenn wir dies berücksichtigen Pa = Pd Na und Pb = Pc da die Prozesse AD und BC isobar sind, dh unter dem gleichen Druck.
Da die Prozesse AB und CD adiabatisch sind, ist das Poisson-Verhältnis für beide Prozesse erfüllt:
Wo Gamma stellt den adiabatischen Quotienten dar, dh den Quotienten zwischen der Wärmekapazität bei konstantem Druck und der Wärmekapazität bei konstantem Volumen.
Unter Verwendung dieser Beziehungen und der Beziehung aus der idealen Gaszustandsgleichung können wir einen alternativen Ausdruck für das Poisson-Verhältnis erhalten:
Woher wissen wir das? Pa = Pd Na und Pb = Pc Durch Ersetzen und Teilen von Mitglied zu Mitglied wird die folgende Beziehung zwischen den Temperaturen erhalten:
Wenn jedes Mitglied der vorherigen Gleichung von der Einheit subtrahiert wird, die Differenz gelöst wird und die Terme angeordnet sind, kann gezeigt werden, dass:
Der Ausdruck, der für die Effizienz des Brayton-Zyklus als Funktion der Temperaturen erhalten wird, kann umgeschrieben werden, um als Funktion des Quotienten des Drucks am Auslass und Einlass des Kompressors formuliert zu werden.
Dies wird erreicht, wenn das Poisson-Verhältnis zwischen den Punkten A und B als Funktion von Druck und Temperatur bekannt ist, wobei erhalten wird, dass die Effizienz des Zyklus wie folgt ausgedrückt wird:
Ein typisches Druckverhältnis ist 8. In diesem Fall hat der Brayton-Zyklus eine theoretische Ausbeute von 45%..
Der Brayton-Zyklus als Modell wird auf Gasturbinen angewendet, die in thermoelektrischen Anlagen eingesetzt werden, um die Stromerzeuger zu bewegen.
Es ist auch ein theoretisches Modell, das sich gut für den Betrieb von Turboprop-Triebwerken eignet, die in Flugzeugen verwendet werden, aber in Flugzeugturbojets überhaupt nicht anwendbar ist..
Wenn Sie die von der Turbine erzeugte Arbeit maximieren möchten, um die Generatoren oder Propeller eines Flugzeugs zu bewegen, wird der Brayton-Zyklus angewendet..
Bei Flugzeugturbojets hingegen ist es nicht interessant, die kinetische Energie der Verbrennungsgase in Arbeit umzuwandeln, die gerade ausreicht, um den Turbolader wieder aufzuladen.
Im Gegenteil, es ist wichtig, die höchstmögliche kinetische Energie des ausgestoßenen Gases zu erhalten, damit nach dem Prinzip der Wirkung und Reaktion der Impuls des Flugzeugs erhalten wird..
Eine in thermoelektrischen Kraftwerken verwendete Gasturbine hat am Kompressorausgang einen Druck von 800 kPa. Die einströmende Gastemperatur ist Umgebungstemperatur und beträgt 25 Grad Celsius, und der Druck beträgt 100 kPa.
In der Brennkammer steigt die Temperatur auf 1027 Grad Celsius, um in die Turbine zu gelangen.
Bestimmen Sie den Kreislaufwirkungsgrad, die Gastemperatur am Kompressorausgang und die Gastemperatur am Turbinenausgang.
Da wir den Druck des Gases am Auslass des Kompressors haben und wissen, dass der Eingangsdruck Atmosphärendruck ist, ist es möglich, das Druckverhältnis zu erhalten:
r = Pb / Pa = 800 kPa / 100 KPa = 8
Da das Gas, mit dem die Turbine arbeitet, ein Gemisch aus Luft und Propangas ist, wird der adiabatische Koeffizient für ein zweiatomiges ideales Gas angewendet, dh ein Gamma von 1,4.
Der Wirkungsgrad würde dann wie folgt berechnet:
Wo wir die Beziehung angewendet haben, die den Wirkungsgrad des Brayton-Zyklus als Funktion des Druckverhältnisses im Kompressor angibt.
Um die Temperatur am Auslass des Kompressors oder die gleiche Temperatur zu bestimmen, mit der das Gas in die Brennkammer eintritt, wenden wir das Verhältnis des Wirkungsgrads zu den Einlass- und Auslasstemperaturen des Kompressors an.
Wenn wir aus diesem Ausdruck nach der Temperatur Tb auflösen, erhalten wir:
Als Daten für die Übung haben wir, dass nach der Verbrennung die Temperatur auf 1027 Grad Celsius steigt, um in die Turbine einzutreten. Ein Teil der Wärmeenergie des Gases wird zum Bewegen der Turbine verwendet, daher muss die Temperatur an ihrem Auslass niedriger sein.
Um die Temperatur am Auslass der Turbine zu berechnen, verwenden wir eine Beziehung zwischen der zuvor erhaltenen Temperatur:
Von dort lösen wir nach Td, um die Temperatur am Auslass der Turbine zu erhalten. Nach Durchführung der Berechnungen beträgt die erhaltene Temperatur:
Td = 143,05 Grad Celsius.
Eine Gasturbine folgt dem Brayton-Zyklus. Das Druckverhältnis zwischen Kompressoreinlass und -auslass beträgt 12.
Nehmen Sie eine Umgebungstemperatur von 300 K an. Als zusätzliche Daten ist bekannt, dass die Temperatur des Gases nach der Verbrennung (vor dem Eintritt in die Turbine) 1000 K beträgt.
Bestimmen Sie die Temperatur am Auslass des Kompressors und die Temperatur am Auslass der Turbine. Bestimmen Sie auch, wie viele Kilogramm Gas pro Sekunde durch die Turbine zirkulieren, und wissen Sie, dass ihre Leistung 30 KW beträgt.
Nehmen Sie die spezifische Wärme des Gases als konstant an und nehmen Sie ihren Wert bei Raumtemperatur an: Cp = 1,0035 J / (kg K).
Es sei auch angenommen, dass der Kompressionswirkungsgrad im Kompressor und der Dekompressionswirkungsgrad in der Turbine 100% beträgt, was eine Idealisierung ist, da in der Praxis immer Verluste auftreten..
Um die Temperatur am Kompressorausgang zu bestimmen und die Einlasstemperatur zu kennen, müssen wir uns daran erinnern, dass es sich um eine adiabatische Kompression handelt, damit das Poisson-Verhältnis für den AB-Prozess angewendet werden kann.
Für jeden thermodynamischen Zyklus entspricht das Netz immer der im Zyklus ausgetauschten Nettowärme..
Das Netzwerk pro Betriebszyklus kann dann als Funktion der in diesem Zyklus zirkulierenden Gasmasse und der Temperaturen ausgedrückt werden.
In diesem Ausdruck m ist die Masse des Gases, das in einem Betriebszyklus durch die Turbine zirkuliert und Vgl spezifische Wärme.
Wenn wir die Ableitung in Bezug auf die Zeit des vorherigen Ausdrucks nehmen, erhalten wir die mittlere Nettoleistung als Funktion des Massenstroms.
Aufräumen m Punkt, Wenn wir die Temperaturen, die Leistung und die Wärmekapazität des Gases ersetzen, erhalten wir einen Massenstrom von 1578,4 kg / s.
Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.