
Bogenmaß (Geometrie), Arten von Bögen, Beispiele
Das Bogen, In der Geometrie ist es jede gekrümmte Linie, die zwei Punkte verbindet. Eine gekrümmte Linie ist im Gegensatz zu einer geraden Linie eine Linie, deren Richtung an jedem Punkt darauf unterschiedlich ist. Das Gegenteil eines Bogens ist ein Segment, da dies ein gerader Abschnitt ist, der zwei Punkte verbindet.
Der in der Geometrie am häufigsten verwendete Bogen ist der Umfangsbogen. Andere gebräuchliche Bögen sind der Parabolbogen, der Ellipsenbogen und der Oberleitungsbogen. Die Bogenform wird in der Architektur auch häufig als dekoratives und strukturelles Element verwendet. Dies ist der Fall bei den Stürzen der Türen und Fenster sowie der Brücken und Aquädukte.

Artikelverzeichnis
- 1 Der Bogen und sein Maß
- 2 Arten von Bögen
- 2.1 Kreisbogen
- 2.2 Parabolbogen
- 2.3 Oberleitungsbogen
- 2.4 Ellipsentrainer
- 3 Beispiele für Bögen
- 3.1 Beispiel 1
- 3.2 Beispiel 2
- 4 Referenzen
Der Bogen und sein Maß
Das Maß eines Bogens ist seine Länge, die von der Art der Kurve abhängt, die die beiden Punkte verbindet, und von ihrer Position..
Die Länge eines Kreisbogens ist eine der am einfachsten zu berechnenden, da die Länge des gesamten Bogens oder Umfangs eines Umfangs bekannt ist.
Der Umfang eines Kreises beträgt zwei Pi mal dein radio: p = 2 π R.. Das wissen Sie, wenn Sie die Länge berechnen möchten s eines kreisförmigen Winkelbogens α (gemessen im Bogenmaß) und Radius R., es wird ein Verhältnis angewendet:
(s / p) = (α / 2 π)
Dann räumen s aus dem vorherigen Ausdruck und Ersetzen des Umfangs p durch seinen Ausdruck als Funktion des Radius R., du hast:
s = (α / 2 π) p = (α / 2 π) (2 π R) = α R..
Das heißt, das Maß eines Kreisbogens ist das Produkt seiner Winkelöffnung mal dem Radius des Kreisbogens.
Für einen Bogen im Allgemeinen ist das Problem komplizierter, bis zu dem Punkt, dass die großen Denker der Antike bestätigten, dass es eine unmögliche Aufgabe war..
Erst mit dem Aufkommen der Differential- und Integralrechnung im Jahre 1665 wurde das Problem der Messung eines Bogens zufriedenstellend gelöst.
Vor der Erfindung der Differentialrechnung konnten Lösungen nur unter Verwendung von polygonalen Linien oder Umfangsbögen gefunden werden, die sich dem wahren Bogen annäherten, aber diese Lösungen waren nicht genau.
Arten von Bögen
Unter dem Gesichtspunkt der Geometrie werden Bögen gemäß der gekrümmten Linie klassifiziert, die zwei Punkte in der Ebene verbindet. Es gibt andere Klassifikationen nach ihrer Verwendung und architektonischen Form.
Kreisbogen
Wenn die Linie, die zwei Punkte der Ebene verbindet, ein Stück des Umfangs eines bestimmten Radius ist, haben wir einen Kreisbogen. Fig. 2 zeigt einen Kreisbogen c mit dem Radius R, der die Punkte A und B verbindet.
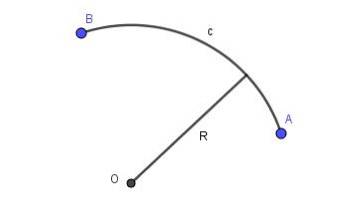
Parabolbogen
Die Parabel ist der Weg, dem ein schräg in die Luft geworfenes Objekt folgt. Wenn die Kurve, die zwei Punkte verbindet, eine Parabel ist, haben wir einen Parabelbogen wie den in Abbildung 3 gezeigten.
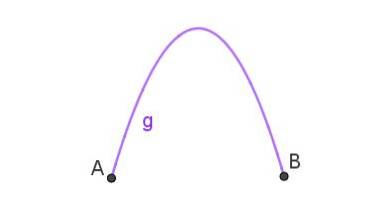
Dies ist die Form des Wasserstrahls, der aus einem nach oben weisenden Schlauch austritt. Der Parabelbogen kann in den Wasserquellen beobachtet werden.

Oberleitungsbogen
Der Oberleitungsbogen ist ein weiterer natürlicher Bogen. Die Oberleitung ist die Kurve, die sich auf natürliche Weise bildet, wenn eine Kette oder ein Seil lose an zwei getrennten Punkten hängt.
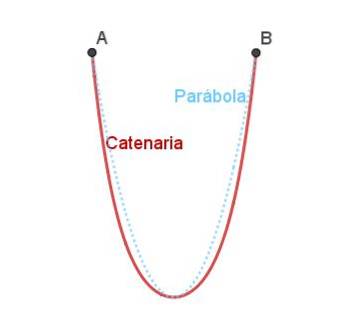
Die Oberleitung ähnelt der Parabel, ist jedoch nicht genau die gleiche wie in Abbildung 4.
Der umgekehrte Oberleitungsbogen wird in der Architektur als Strukturelement mit hoher Druckfestigkeit verwendet. Tatsächlich kann gezeigt werden, dass es der stärkste Bogentyp aller möglichen Formen ist..
Um einen soliden Oberleitungsbogen zu bauen, kopieren Sie einfach die Form eines hängenden Seils oder einer Kette. Anschließend wird die kopierte Form umgedreht, um sie auf dem Tür- oder Fenstersturz zu reproduzieren.
Elliptischer Bogen
Ein Bogen ist elliptisch, wenn die Kurve, die zwei Punkte verbindet, ein Stück oder ein Abschnitt einer Ellipse ist. Die Ellipse ist definiert als der Ort der Punkte, deren Abstand zu zwei gegebenen Punkten immer eine konstante Größe ergibt.
Die Ellipse ist eine Kurve, die in der Natur erscheint: Es ist die Kurve der Flugbahn der Planeten um die Sonne, wie Johannes Kepler im Jahr 1609 demonstrierte.
In der Praxis kann eine Ellipse gezeichnet werden, indem zwei Streben am Boden oder zwei Stifte auf Papier befestigt und eine Schnur daran gebunden werden. Das Seil wird dann mit dem Marker oder Bleistift gespannt und die Kurve wird nachgezeichnet. Ein Stück Ellipse ist ein elliptischer Bogen. Die folgende Animation zeigt, wie die Ellipse gezeichnet wird:
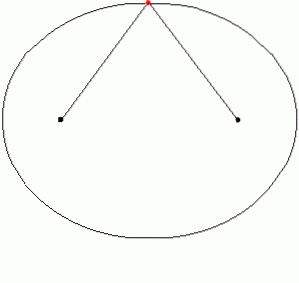
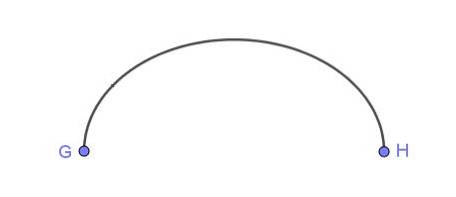
Fig. 6 zeigt einen elliptischen Bogen, der die Punkte G und H verbindet.
Beispiele für Bögen
Die folgenden Beispiele beziehen sich auf die Berechnung des Umfangs einiger bestimmter Bögen.
Beispiel 1
Fig. 7 zeigt ein Fenster, das in einem geschnittenen Kreisbogen fertiggestellt ist. Die in der Abbildung gezeigten Abmessungen sind in Fuß angegeben. Berechnen Sie die Länge des Bogens.
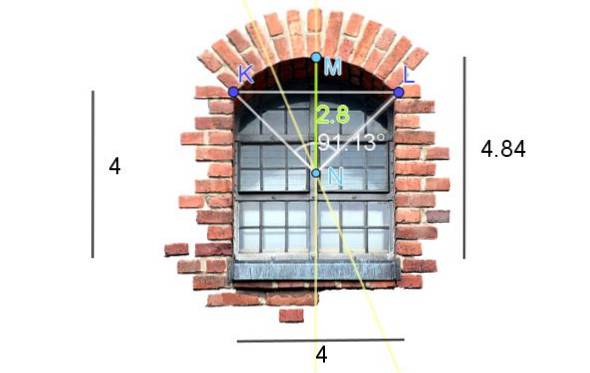
Um den Mittelpunkt und den Radius des Kreisbogens des Fenstersturzes zu erhalten, werden die folgenden Konstruktionen auf dem Bild vorgenommen:
-Das Segment KL wird gezeichnet und seine Winkelhalbierende wird gezeichnet.
-Danach befindet sich der höchste Punkt des Sturzes, den wir M nennen. Als nächstes wird das Segment KM betrachtet und seine Mittlerin verfolgt..
Der Achsenabschnitt der beiden Winkelhalbierenden ist der Punkt N und auch der Mittelpunkt des Kreisbogens.
-Nun müssen wir die Länge des Segments NM messen, die mit dem Radius R des Kreisbogens zusammenfällt: R = 2,8 Fuß.
-Um die Länge des Bogens zusätzlich zum Radius zu kennen, muss der Winkel bekannt sein, den der Bogen bildet. Dies kann mit zwei Methoden bestimmt werden, entweder mit einem Winkelmesser oder alternativ mit Trigonometrie.
Im gezeigten Fall beträgt der vom Bogen gebildete Winkel 91,13º, der in Bogenmaß umgerechnet werden muss:
91,13º = 91,13º * π / 180º = 1,59 Bogenmaß
Schließlich berechnen wir die Länge s des Bogens unter Verwendung der Formel s = α R..
s = 1,59 * 2,8 Fuß = 4,45 Fuß
Beispiel 2
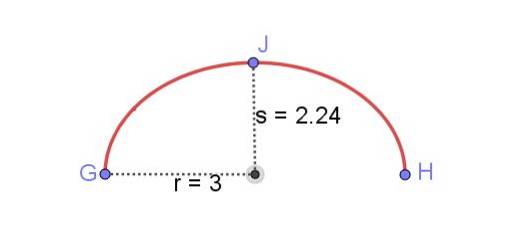
Ermitteln Sie die Länge des in Abbildung 8 gezeigten elliptischen Bogens unter Kenntnis der Semi-Major-Achse r und die semi-minor Achse s der Ellipse.
Das Ermitteln der Länge einer Ellipse war lange Zeit eines der schwierigsten Probleme in der Mathematik. Sie können Lösungen erhalten, die durch elliptische Integrale ausgedrückt werden. Um jedoch einen numerischen Wert zu erhalten, müssen Sie diese Integrale in Potenzreihen erweitern. Ein genaues Ergebnis würde unendlich viele Terme dieser Reihen erfordern.
Glücklicherweise fand das hinduistische mathematische Genie Ramanujan, das zwischen 1887 und 1920 lebte, eine Formel, die sich dem Umfang einer Ellipse sehr genau annähert:
Umfang einer Ellipse = π [3 (r + s) - √ ((3r + s) (r + 3s))]
Der Umfang einer Ellipse mit r = 3 cm und s = 2,24 cm beträgt 16,55 cm. Der gezeigte elliptische Bogen hat jedoch die Hälfte dieses Wertes:
Länge des elliptischen Bogens GH = 8,28 cm.
Verweise
- Clemens S. 2008. Geometrie und Trigonometrie. Pearson Ausbildung.
- García F. Numerische Prozeduren in Java. Länge einer Ellipse. Wiederhergestellt von: sc.ehu.es
- Dynamische Geometrie. Bögen. Aus geometriadinamica.es wiederhergestellt
- Piziadas. Ellipsen und Parabeln um uns herum. Wiederhergestellt von: piziadas.com
- Wikipedia. Bogen (Geometrie). Wiederhergestellt von: es.wikipedia.com


Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.