
Factorial Rig Definition, Formeln und Übungen
Das Fakultäts-Rig Es ist eine einfache Maschine, die aus einer Anordnung von Riemenscheiben mit einem Multiplikationseffekt der Kraft besteht. Auf diese Weise kann eine Last angehoben werden, indem nur das Äquivalent eines Bruchteils des Gewichts auf das freie Ende des Seils aufgebracht wird..
Es besteht aus zwei Sätzen von Riemenscheiben: einer, der an einem Träger befestigt ist, und einer, der die resultierende Kraft auf die Last ausübt. Die Riemenscheiben sind auf einem im Allgemeinen metallischen Rahmen montiert, der sie hält.
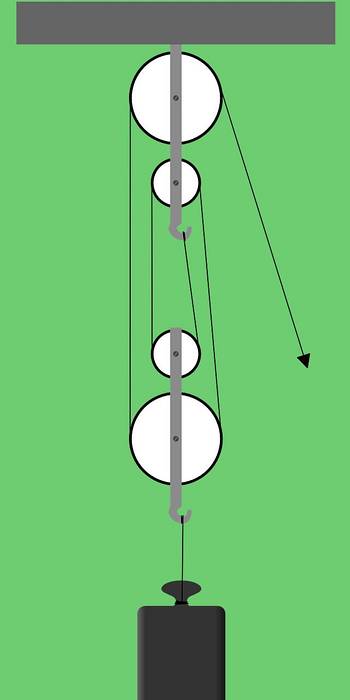
Abbildung 1 zeigt eine Fakultätsanlage, die aus zwei Gruppen zu je zwei Riemenscheiben besteht. Diese Art der Riemenscheibenanordnung wird auch genannt serielle Takelage oder Hebezeuge.
Artikelverzeichnis
- 1 Formeln für die faktorielle Takelage
- 1.1 Fall 1: Eine bewegliche und eine feste Riemenscheibe
- 1.2 Fall 2: Zwei bewegliche und zwei feste Riemenscheiben
- 1.3 Allgemeiner Fall: n bewegliche Riemenscheiben und n feste Riemenscheiben
- 2 Gelöste Übungen
- 2.1 Übung 1
- 2.2 Übung 2
- 2.3 Übung 3
- 3 Referenzen
Formeln für die faktorielle Takelage
Fall 1: Eine mobile und eine feste Riemenscheibe
Um zu verstehen, warum diese Anordnung die ausgeübte Kraft multipliziert, beginnen wir mit dem einfachsten Fall, der aus einer festen Riemenscheibe und einer beweglichen Riemenscheibe besteht..

In Abbildung 2 ist eine Riemenscheibe A mittels einer Stütze an der Decke befestigt. Die Riemenscheibe A kann sich frei um ihre Achse drehen. Wir haben auch eine Riemenscheibe B, an deren Riemenscheibenwelle eine Halterung angebracht ist, auf die die Last gelegt wird. Die Riemenscheibe B kann sich nicht nur frei um ihre Achse drehen, sondern auch vertikal bewegen.
Angenommen, wir befinden uns in einer Gleichgewichtssituation. Betrachten Sie die auf die Riemenscheibe B einwirkenden Kräfte. Die Achse der Riemenscheibe B trägt ein Gesamtgewicht P, das nach unten gerichtet ist. Wenn dies die einzige Kraft auf die Riemenscheibe B wäre, würde sie fallen, aber wir wissen, dass das Seil, das durch diese Riemenscheibe verläuft, auch zwei Kräfte ausübt, nämlich T1 und T2, die nach oben gerichtet sind..
Damit ein Translationsgleichgewicht besteht, müssen die beiden Aufwärtskräfte gleich dem Gewicht sein, das von der Achse der Riemenscheibe B getragen wird.
T1 + T2 = P.
Da sich aber auch die Riemenscheibe B im Rotationsgleichgewicht befindet, ist T1 = T2. Die Kräfte T1 und T2 ergeben sich aus der auf die Saite ausgeübten Spannung, die als T bezeichnet wird.
Daher ist T1 = T2 = T. Einsetzen in die vorherige Gleichung bleibt es:
T + T = P.
2T = P.
Was darauf hinweist, dass die auf das Seil ausgeübte Spannung nur die Hälfte des Gewichts beträgt:
T = P / 2
Wenn die Last beispielsweise 100 kg wäre, würde es ausreichen, am freien Ende des Seils eine Kraft von 50 kg aufzubringen, um die Last mit einer konstanten Geschwindigkeit anzuheben..
Fall 2: Zwei bewegliche und zwei feste Riemenscheiben
Betrachten wir nun die Spannungen und Kräfte, die auf eine Baugruppe wirken, die aus zwei Anordnungen der Stützen A und B mit jeweils zwei Riemenscheiben besteht..

Die Stütze B hat die Möglichkeit, sich vertikal zu bewegen, und die auf sie einwirkenden Kräfte sind:
- Das Gewicht P der Last zeigt senkrecht nach unten.
- Zwei Spannungen an der großen Riemenscheibe und zwei Spannungen an der kleinen Riemenscheibe. Insgesamt vier Spannungen, die alle nach oben zeigen.
Für ein Translationsgleichgewicht ist es erforderlich, dass die vertikal nach oben weisenden Kräfte dem Wert entsprechen, der der nach unten zeigenden Last entspricht. Das heißt, es muss erfüllt sein:
T + T + T + T = P.
Das heißt, 4 T = P.
Daraus folgt, dass die am freien Ende des Seils ausgeübte Kraft T aufgrund der Last, die angehoben werden soll, nur ein Viertel des Gewichts beträgt. T = P / 4.
Mit diesem Wert für die Spannung T kann die Last statisch gehalten werden oder mit konstanter Geschwindigkeit ansteigen. Wenn eine Spannung größer als dieser Wert angelegt würde, würde die Last nach oben beschleunigen, eine Bedingung, die erforderlich ist, um sie aus dem Ruhezustand zu bringen..
Allgemeiner Fall: n bewegliche Riemenscheiben und n feste Riemenscheiben
Gemäß dem, was in den vorhergehenden Fällen gesehen wurde, gibt es für jede Riemenscheibe der mobilen Baugruppe ein paar Aufwärtskräfte, die von dem Seil ausgeübt werden, das durch die Riemenscheibe verläuft. Diese Kraft kann jedoch nichts anderes sein als die Spannung, die am freien Ende auf das Seil ausgeübt wird.
Damit gibt es für jede Riemenscheibe der mobilen Baugruppe eine vertikale Kraft nach oben, die 2T entspricht. Da sich jedoch n Riemenscheiben in der beweglichen Baugruppe befinden, ergibt sich folgende Gesamtkraft, die vertikal nach oben zeigt:
2 n T.
Für ein vertikales Gleichgewicht ist Folgendes erforderlich:
2 n T = P.
daher ist die am freien Ende ausgeübte Kraft:
T = P / (2 n)
In diesem Fall kann gesagt werden, dass die auf die Last ausgeübte Kraft T 2 n-mal multipliziert wird.
Wenn wir zum Beispiel ein Fakultätsgerät mit 3 festen und 3 beweglichen Riemenscheiben hätten, wäre die Anzahl n gleich 3. Wenn andererseits die Last P = 120 kg wäre, wäre die am freien Ende ausgeübte Kraft T = 120 kg / (2 · 3) = 20 kg.
Gelöste Übungen
Übung 1
Stellen Sie sich ein Fakultätsgerät vor, das aus zwei festen und zwei beweglichen Riemenscheiben besteht. Die maximale Spannung, der das Seil standhalten kann, beträgt 60 kg. Bestimmen Sie, welche maximale Last maximal platziert werden kann.
Lösung
Wenn die Last in Ruhe ist oder sich mit konstanter Geschwindigkeit bewegt, hängt ihr Gewicht P mit der Spannung T zusammen, die mittels der folgenden Beziehung auf das Seil ausgeübt wird:
P = 2 n T.
Da es sich um ein Rig mit zwei beweglichen und zwei festen Riemenscheiben handelt, ist n = 2.
Die maximale Last, die platziert werden kann, wird erhalten, wenn T den maximal möglichen Wert hat, der in diesem Fall 60 kg beträgt.
Maximale Belastung = 2 * 2 * 60 kg = 240 kg
Übung 2
Finden Sie die Beziehung zwischen der Seilspannung und dem Gewicht der Last in einem faktoriellen Rig mit zwei Riemenscheiben, in dem die Last mit einer Beschleunigung von beschleunigt wird.
Lösung
Der Unterschied dieses Beispiels zu dem, was bisher gesehen wurde, besteht darin, dass die Dynamik des Systems berücksichtigt werden muss. Also schlagen wir Newtons zweites Gesetz vor, um die gewünschte Beziehung zu finden.

In Abbildung 4 zeichnen wir die Kräfte aufgrund der Spannung T des Seils gelb. Der bewegliche Teil des Hebezeugs hat eine Gesamtmasse M. Als Bezugssystem nehmen wir eines auf Höhe der ersten festen Riemenscheibe und positiv nach unten.
Y1 ist die niedrigste Position der Riemenscheibenwelle.
Wir wenden das zweite Newtonsche Gesetz an, um die Beschleunigung a1 des beweglichen Teils des Rigs zu bestimmen:
-4 T + Mg = M a1
Da das Gewicht der Last P = Mg ist, wobei g die Erdbeschleunigung ist, kann die obige Beziehung geschrieben werden:
-4T + P = P (a1 / g)
Wenn wir die Spannung bestimmen wollten, die auf das Seil ausgeübt wird, wenn eine bestimmte Gewichtslast P mit der Beschleunigung a1 beschleunigt wird, dann würde die vorherige Beziehung folgendermaßen aussehen:
T = P (1 - a1 / g) / 4
Beachten Sie, dass a1 = 0 ist, wenn das System in Ruhe ist oder sich mit konstanter Geschwindigkeit bewegt, und wir denselben Ausdruck wiederherstellen würden, den wir in Fall 2 erhalten haben.
Übung 3
In diesem Beispiel wird dieselbe Takelage aus Übung 1 mit demselben Seil verwendet, das maximal 60 kg Spannung trägt. Eine bestimmte Last wird angehoben und in 0,5 s unter Verwendung der maximalen Spannung des Seils aus dem Ruhezustand auf 1 m / s beschleunigt. Finden Sie das maximale Gewicht der Ladung.
Lösung
Wir werden die in Übung 2 erhaltenen Ausdrücke und das Bezugssystem von 4 verwenden, in dem die positive Richtung vertikal nach unten ist.
Die Beschleunigung der Last beträgt a1 = (-1 m / s - 0 m / s) / 0,5 s = -2 m / s ^ 2.
Das Gewicht der Last in Kilogramm Kraft ist gegeben durch
P = 4 T / (1 - a1 / g)
P = 4 · 60 kg / (1 + 2 / 9,8) = 199,3 kg
Dies ist das maximal mögliche Gewicht der Last, ohne dass das Seil bricht. Es ist zu beachten, dass der erhaltene Wert kleiner ist als der in Beispiel 1 erhaltene, bei dem angenommen wurde, dass die Last eine Beschleunigung von Null aufweist, dh in Ruhe oder mit konstanter Geschwindigkeit..
Verweise
- Sears, Zemansky. 2016. Universitätsphysik mit moderner Physik. 14 .. Ed. Volume 1. 101-120.
- Resnick, R. (1999). Körperlich. Vol. 1. 3rd Ed. In Spanisch. Compañía Editorial Continental S.A. de C.V. 87-103.
- Giancoli, D. 2006. Physik: Prinzipien mit Anwendungen. 6 .. Ed. Prentice Hall. 72 - 96.
- Hewitt, Paul. 2012. Konzeptionelle Physik. 5 .. Ed. Pearson. 38-61.
- Serway, R., Jewett, J. (2008). Physik für Wissenschaft und Technik. Band 1. 7 .. Ed. Lernen einbinden. 100 - 119.



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.