
Konzepte, Methoden und Beispiele für die Netzanalyse
Das Netzanalyse ist eine Technik, die verwendet wird, um flache elektrische Schaltkreise zu lösen. Dieses Verfahren kann auch in der Literatur unter den Methodennamen der Stromkreise oder Methode von Maschenströme (oder Schleife).
Die Grundlage dieser und anderer Methoden zur Analyse elektrischer Schaltkreise sind die Kirchhoffschen Gesetze und das Ohmsche Gesetz. Kirchhoffs Gesetze wiederum drücken zwei sehr wichtige Prinzipien der Erhaltung in der Physik für isolierte Systeme aus: Sowohl die elektrische Ladung als auch die Energie werden erhalten..

Einerseits hängt die elektrische Ladung mit dem Strom zusammen, der die in Bewegung befindliche Ladung ist, während in einem Stromkreis die Energie mit der Spannung verbunden ist, die das Mittel ist, das für die Ausführung der Arbeit verantwortlich ist, die zum Halten der Ladung erforderlich ist Bewegung..
Diese Gesetze, die auf eine flache Schaltung angewendet werden, erzeugen einen Satz simultaner Gleichungen, die gelöst werden müssen, um die Strom- oder Spannungswerte zu erhalten..
Das Gleichungssystem kann mit bekannten Analysetechniken gelöst werden, wie z Cramers Regel, Dies erfordert die Berechnung von Determinanten, um die Lösung des Systems zu erhalten.
Abhängig von der Anzahl der Gleichungen werden sie mit einem wissenschaftlichen Taschenrechner oder einer mathematischen Software gelöst. Im Internet stehen auch viele Optionen zur Verfügung.
Artikelverzeichnis
- 1 Wichtige Begriffe
- 2 Methoden
- 2.1 - Schritte zum Anwenden der Netzanalyse
- 3 Gelöste Übungen
- 3.1 - Beispiel 1
- 3.2 - Beispiel 2
- 4 Referenzen
Wichtige Begriffe
Bevor wir erklären, wie es funktioniert, definieren wir zunächst folgende Begriffe:
Ast: Abschnitt mit einem Schaltungselement.
Knoten: Punkt, der zwei oder mehr Zweige verbindet.
Band: ist ein geschlossener Teil eines Stromkreises, der am selben Knoten beginnt und endet.
Gittergewebe: Schleife, die keine andere Schleife enthält (essentielles Netz).
Methoden
Die Netzanalyse ist eine allgemeine Methode zur Lösung von Schaltkreisen, deren Elemente in Reihe, parallel oder gemischt geschaltet sind, dh wenn die Art der Verbindung nicht klar unterschieden wird. Die Schaltung muss flach sein, oder es muss zumindest möglich sein, sie als solche neu zu zeichnen.
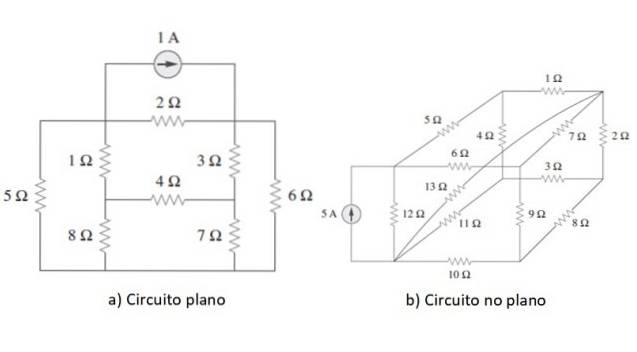
Ein Beispiel für jeden Schaltungstyp ist in der obigen Abbildung dargestellt. Sobald der Punkt geklärt ist, werden wir die Methode zunächst im nächsten Abschnitt auf eine einfache Schaltung als Beispiel anwenden, aber zuerst werden wir kurz die Gesetze von Ohm und Kirchhoff überprüfen.
Ohm'sches Gesetz: Sein V. die Spannung, R. Widerstand e ich der Strom des ohmschen Widerstandselements, bei dem Spannung und Strom direkt proportional sind, wobei der Widerstand die Proportionalitätskonstante ist:
V = I.R.
Kirchhoffs Spannungsgesetz (LKV): In jedem geschlossenen Pfad, der nur in eine Richtung zurückgelegt wird, ist die algebraische Summe der Spannungen Null. Dies schließt Spannungen aufgrund von Quellen, Widerständen, Induktivitäten oder Kondensatoren ein: ∑ E = ∑ R.ich. ich
Kirchhoffs Gesetz der Strömung (LKC): An jedem Knoten ist die algebraische Summe der Ströme Null, wobei berücksichtigt wird, dass den eingehenden Strömen ein Vorzeichen zugewiesen wird und denen, die ein anderes verlassen. Auf diese Weise: ∑ I = 0.
Bei der Maschenstrommethode ist es nicht erforderlich, das aktuelle Kirchhoffsche Gesetz anzuwenden, was zu weniger zu lösenden Gleichungen führt.
- Schritte zum Anwenden der Netzanalyse
Wir beginnen mit der Erläuterung der Methode für eine 2-Mesh-Schaltung. Das Verfahren kann dann für größere Schaltungen erweitert werden.
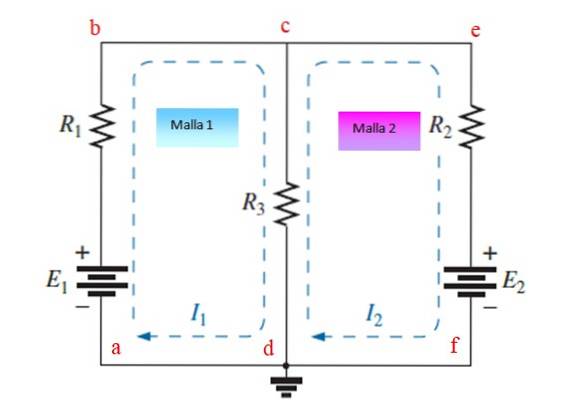
Schritt 1
Weisen Sie jedem Netz unabhängige Ströme zu und zeichnen Sie sie. In diesem Beispiel sind dies Ströme ich1 und ichzwei. Sie können im oder gegen den Uhrzeigersinn gezeichnet werden.
Schritt 2
Wenden Sie das Kirchhoffsche Spannungsgesetz (LTK) und das Ohmsche Gesetz auf jedes Netz an. Potenzielle Tropfen erhalten ein Vorzeichen (-), während Anstiege ein Vorzeichen (+) erhalten..
Mesh abcda
Ausgehend von Punkt a und in Richtung des Stroms finden wir einen möglichen Anstieg der Batterie E1 (+) und dann einen Abfall von R.1 (-) und dann noch ein Tropfen in R.3 (-).
Gleichzeitig ist der Widerstand R.3 wird auch vom Strom I durchquertzwei, aber in die entgegengesetzte Richtung repräsentiert es daher einen Anstieg (+). Die erste Gleichung sieht folgendermaßen aus:
UND1-R.1.ich1 -R.3.ich1 + R.3.ichzwei = 0
Dann wird es berücksichtigt und die Begriffe werden neu gruppiert:
- (R.1+R.3) ICH1 +R.3ichzwei = -E1 (Gleichung 1)
Cefdc-Netz
Ausgehend vom Punkt und und der Richtung des Stroms folgend, wird ein Potentialabfall in gefunden R.zwei (-), ein weiterer Besuch UNDzwei, da der Strom durch den + Pol der Batterie eintritt und schließlich wieder einfällt R.3 (-), gleichzeitig der Strom ich1 durchquert R.3 in die entgegengesetzte Richtung (+).
Die zweite Gleichung mit den angegebenen Zeichen sieht folgendermaßen aus:
- R.zwei ichzwei - UNDzwei -R.3 ichzwei +R.3 ich1= 0
R.3ich1 - (R.zwei +R.3) ichzwei = E.zwei (Gleichung 2)
Beachten Sie, dass es zwei Gleichungen mit den beiden Unbekannten I gibt1 und ichzwei.
Schritt 3
Das so gebildete Gleichungssystem wird dann gelöst.
Gelöste Übungen
Zu Beginn ist es wichtig, Folgendes zu berücksichtigen:
-Schleifenströmen oder Maschenströmen kann eine beliebige Adresse zugewiesen werden.
-Jedem wesentlichen Netz - oder "Fenster" -, das der Stromkreis hat, muss ein Strom zugewiesen werden.
-Netzströme werden mit einem Großbuchstaben gekennzeichnet, um sie von Strömen zu unterscheiden, die durch Zweige zirkulieren, obwohl in einigen Fällen der Strom, der durch einen Zweig zirkuliert, der gleiche sein kann wie der von Maschenströmen.
- Beispiel 1
Finden Sie die Ströme, die durch jeden Widerstand in der Schaltung von 3 fließen, wenn die Elemente die folgenden Werte haben:
R.1 = 20 Ω; R.zwei = 30 Ω; R.3 = 10 Ω; UND1 = 12 V; UNDzwei = 18 V.
Lösung
Zunächst müssen die Maschenströme I zugeordnet werden1 und ichzwei Nehmen Sie das im vorherigen Abschnitt ermittelte Gleichungssystem und ersetzen Sie die in der Anweisung angegebenen Werte:
- (R.1+R.3) ICH1 +R.3ichzwei = -E1 (Gleichung 1)
R.3ich1 - (R.zwei +R.3) ichzwei = E.zwei (Gleichung 2)
-
-(20 + 30) ich1 + 10Izwei = -12
10I1 - (30 + 10) I.zwei = 18
--
-fünfzigich1 + 10Izwei = -12
10I1 - 40 I.zwei = 18
Da es sich um ein 2 x 2-Gleichungssystem handelt, kann es leicht durch Reduktion gelöst werden, indem die zweite Gleichung mit 5 multipliziert wird, um das Unbekannte zu beseitigen ich1::
-fünfzigich1 + 10 I.zwei = -12
50I1 - 200 I.zwei = 90
-
-190 I.zwei= 78
ichzwei = - 78/180 A = - 0,41 A.
Sofort löscht sich der Strom ich1 aus einer der ursprünglichen Gleichungen:
ich1 = (18 + 40 I.zwei) / 10 = (18 + 40 x (-0,41)) / 10 = 0,16 A.
Das negative Vorzeichen im Strom ichzwei bedeutet, dass der Strom in Masche 2 in der entgegengesetzten Richtung zu der gezogenen zirkuliert.
Die Ströme in jedem Widerstand sind wie folgt:
Für den Widerstand R.1 Der Strom zirkuliert ich1 = 0,16 A. im Sinne von Widerstand R.zwei Der Strom zirkuliert ichzwei = 0,41 A. in die entgegengesetzte Richtung zu der gezeichneten und durch den Widerstand R.3 zirkulieren ich3 = 0,16- (-0,41) A = 0,57 A. Nieder.
Systemlösung nach Cramer
In Matrixform kann das System wie folgt gelöst werden:
Schritt 1: Berechnen Sie Δ

Schritt 2: Berechnen Sie Δ1
Die erste Spalte wird durch die unabhängigen Terme des Gleichungssystems ersetzt, wobei die Reihenfolge beibehalten wird, in der das System ursprünglich vorgeschlagen wurde:

Schritt 3: Berechne ich1
ich1 = Δ1/ Δ = 300/1900 = 0,16 A.
Schritt 4: Berechnen Sie Δzwei

ichzwei = Δzwei/ Δ = -780/1900 = -0,41 A.
- Beispiel 2
Bestimmen Sie den Strom und die Spannungen durch jeden Widerstand in der folgenden Schaltung mithilfe der Maschenstrommethode:

Lösung
Die drei Maschenströme werden, wie in der folgenden Abbildung gezeigt, in beliebige Richtungen gezogen. Jetzt werden die Maschen ab einem beliebigen Punkt durchlaufen:
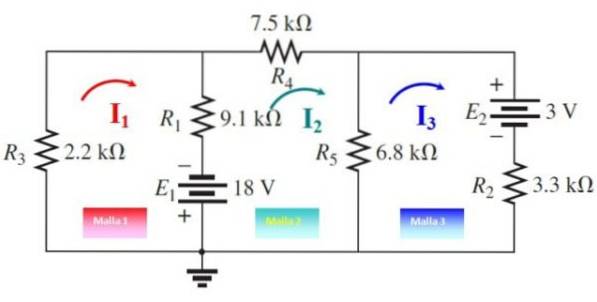
Mesh 1
-9100.I1+18-2200.I1+9100.Izwei= 0
-11300 I.1 + 9100.Izwei = -18
Mesh 2
-(7500 + 6800 + 9100) .Izwei + 9100.I1+6800.I3-18 = 0
9100.I1 - 23400.Izwei + 6800.I3 = 18
Mesh 3
-(6800 + 3300) I.3 + 6800.Izwei - 3 = 0
6800.Izwei - 10100.I3 = 3
Gleichungssystem
-11300 I.1 + 9100.Izwei + 0.I.3= -18
9100.I1 - 23400.Izwei + 6800.I3 = 18
0.I.1 + 6800.Izwei - 10100.I3 = 3
Obwohl die Zahlen groß sind, kann es mit Hilfe eines wissenschaftlichen Taschenrechners schnell gelöst werden. Denken Sie daran, dass die Gleichungen geordnet werden müssen, und fügen Sie Nullen an den Stellen hinzu, an denen das Unbekannte nicht erscheint, wie es hier erscheint.
Die Maschenströme sind:
ich1 = 0,0012 A; ichzwei = -0.00048 A; ich3 = -0.00062 A.
Strömungen ichzwei und ich3 zirkulieren in die entgegengesetzte Richtung zu der in der Figur gezeigten, da sie sich als negativ herausstellten.
Tabelle der Ströme und Spannungen in jedem Widerstand
| Widerstand (Ω) | Strom (Ampere) | Spannung = I.R. (Volt) |
|---|---|---|
| 9100 | ich1 -ichzwei = 0,0012 - (- 0,00048) = 0,00168 | 15.3 |
| 3300 | 0,00062 | 2.05 |
| 2200 | 0,0012 | 2.64 |
| 7500 | 0,00048 | 3,60 |
| 6800 | ichzwei -ich3= -0.00048 - (- 0.00062) = 0.00014 | 0,95 |
Cramers Regellösung
Da es sich um eine große Anzahl handelt, ist es zweckmäßig, die wissenschaftliche Notation zu verwenden, um direkt mit ihnen zu arbeiten.
Berechnung von I.1
Die farbigen Pfeile in der 3 x 3-Determinante geben an, wie die numerischen Werte durch Multiplizieren der angegebenen Werte ermittelt werden. Beginnen wir damit, die der ersten Klammer in der Determinante Δ zu erhalten:
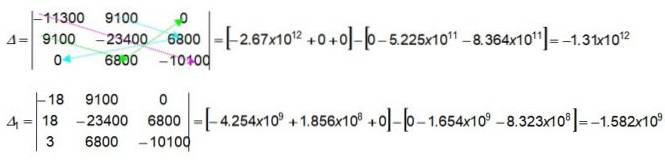
(-11300) x (-23400) x (-10100) = -2,67 x 1012
9100 x 0 x 0 = 0
9100 x 6800 x 0 = 0
Sofort erhalten wir die zweite Klammer in derselben Determinante, die von links nach rechts bearbeitet wird (für diese Klammer wurden die farbigen Pfeile in der Abbildung nicht gezeichnet). Wir laden den Leser ein, dies zu überprüfen:
0 x (-23400) x 0 = 0
9100 x 9100 x (-10100) = -8,364 x 10elf
6800 x 6800 x (-11300) = -5,225 x 10elf
In ähnlicher Weise kann der Leser auch die Werte für die Determinante überprüfen Δ1.
Wichtig: Zwischen beiden Klammern steht immer ein negatives Vorzeichen.
Endlich bekommst du den Strom ich1 durch ich1 = Δ1 / Δ
ich1 = -1,582 x 109/-1,31 x 1012 = 0,0012 A.
Berechnung von I.zwei
Der Vorgang kann zur Berechnung wiederholt werden ichzwei, in diesem Fall zur Berechnung der Determinante Δzwei Die zweite Spalte der Determinante Δ wird durch die Spalte der unabhängigen Terme ersetzt und ihr Wert wird gemäß dem erläuterten Verfahren gefunden.
Da dies jedoch aufgrund der großen Anzahl umständlich ist, insbesondere wenn Sie keinen wissenschaftlichen Taschenrechner haben, ist es am einfachsten, den Wert von zu ersetzen ich1 bereits berechnet, in der folgenden Gleichung und klar:
-11300 I.1 + 9100.Izwei + 0.I.3= -18 → 9100 I.zwei= -18 + 11300 I.1 → I.zwei = -0.00048 A.
Berechnung von I3
Einmal mit den Werten von ich1 und ichzwei in der Hand, die von ich3 direkt durch Substitution gefunden.
Verweise
- Alexander, C. 2006. Grundlagen elektrischer Schaltungen. 3 .. Auflage. Mc Graw Hill.
- Boylestad, R. 2011. Einführung in die Schaltungsanalyse.2da. Auflage. Pearson.
- Figueroa, D. (2005). Reihe: Physik für Wissenschaft und Technik. Band 5. Elektrische Wechselwirkung. Herausgegeben von Douglas Figueroa (USB).
- García, L. 2014. Elektromagnetismus. 2 .. Auflage. Industrielle Universität von Santander.
- Sears, Zemansky. 2016. Universitätsphysik mit moderner Physik. 14 .. Ed. Band 2.



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.