
12 Welleneigenschaften (mit Beispielen)

Das Welleneigenschaften sind die Kennzeichen des Wellenphänomens: Wellenlänge, Frequenz, Täler, Scheitel, Geschwindigkeit, Energie und andere, die wir in diesem Artikel erläutern werden.
In Wellen bewegen sich nicht Teilchen mit der Störung, sondern Energie. Wenn sich eine Welle in einem materiellen Medium ausbreitet, das unter anderem Wasser, Luft oder ein Seil sein kann, bewegen sich die Partikel kaum aus der Gleichgewichtsposition, um nach kurzer Zeit dorthin zurückzukehren.
Die Bewegung wird jedoch von einem Teilchen auf ein anderes übertragen, wodurch jedes von ihnen vibriert. Auf diese Weise die Störung, die wir nennen Welle, Genau wie die Welle der Fans in Stadien, wenn Fußballspiele gespielt werden.
Das Studium der Wellen ist sehr interessant, da wir in einer Welt voller Wellen leben: Licht, Meereswellen, der Klang von Musik und Stimme sind Wellenphänomene, wenn auch unterschiedlicher Natur. Sowohl Licht als auch Ton sind besonders wichtig, da wir sie ständig brauchen, um mit der Außenwelt zu kommunizieren..
Was sind die Eigenschaften der Wellen?
Vibration
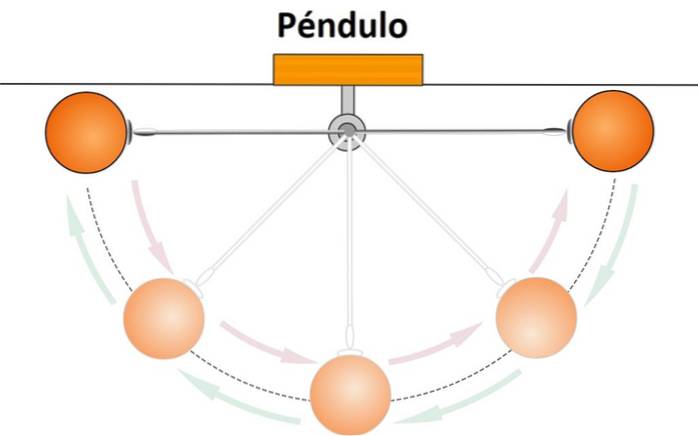
Es ist der vollständige Weg, den ein Teilchen in seiner Hin- und Herbewegung macht. Zum Beispiel hat ein Pendel eine Hin- und Herbewegung, da es ab einem bestimmten Punkt einen Bogen beschreibt, anhält, wenn es eine bestimmte Höhe erreicht, und in seine ursprüngliche Position zurückkehrt..
Ohne Reibung würde diese Bewegung auf unbestimmte Zeit fortgesetzt. Aufgrund der Reibung wird die Bewegung jedoch langsamer und weniger breit, bis das Pendel stoppt..
Wenn eine horizontale gespannte Saite gestört wird, vibrieren die Partikel der Saite in vertikaler Richtung, dh von oben nach unten, während sich die Störung horizontal entlang der Saite ausbreitet.
Schaukelzentrum
Wenn ein Teilchen seine Hin- und Herbewegung ausführt, bewegt es sich um einen bestimmten Punkt, der als Ursprung oder Schwingungszentrum bezeichnet wird..
Im Beispiel des Pendels befindet es sich am tiefsten Punkt im Gleichgewicht und schwingt um es herum, wenn wir es ein wenig von dieser Position trennen. Daher kann dieser Punkt als Mittelpunkt der Schwingung betrachtet werden.
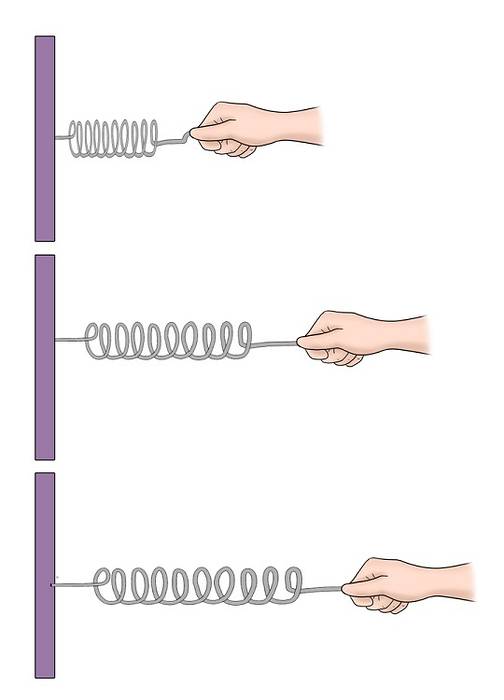
Wir können uns auch eine Feder auf einem horizontalen Tisch vorstellen, der an einem Ende an einer Wand befestigt ist und am anderen Ende einen Block hat. Wenn das Federblocksystem ungestört ist, befindet sich der Block in einer bestimmten Gleichgewichtsposition.
Durch leichtes Zusammendrücken oder Strecken der Feder beginnt das System jedoch, um diese Gleichgewichtsposition herum zu schwingen..
Verlängerung
Dies ist die Entfernung, um die sich das Teilchen nach einiger Zeit vom Schwingungszentrum entfernt. Sie wird in Metern gemessen, wenn das SI International System verwendet wird..
Wenn eine Feder mit einem Block an einem Ende zusammengedrückt oder gedehnt wird, soll sie eine Dehnung von "x" Metern, Zentimetern oder einer anderen Einheit erfahren haben, die zum Messen der Entfernung verwendet wird..
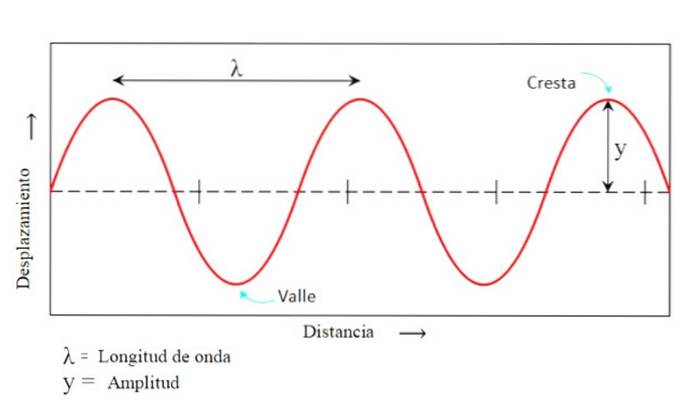
Grate und Täler
Sie sind jeweils der höchste und der niedrigste Punkt, den das Teilchen in Bezug auf die Gleichgewichtsposition y = 0 erreicht (siehe Abbildung 1)..
Amplitude

Dies ist die maximale Entfernung, die das Teilchen vom Schwingungszentrum trennt, und wird auch in Metern angegeben. Es wird bezeichnet als ZU oder als Y.. Dort fällt die Gleichgewichtsposition mit y = 0 zusammen und entspricht den Wellenbergen und -tälern.
Die Amplitude ist ein wichtiger Parameter, da sie sich auf die von der Welle getragene Energie bezieht. Je größer die Amplitude ist, desto größer ist die Energie, wie dies beispielsweise bei Meereswellen der Fall ist.
Knoten
Die Knoten sind die Punkte, an denen das Teilchen das Schwingungszentrum oder die Gleichgewichtsposition passiert..
Zyklus
Dies nennt man eine vollständige Schwingung, wenn das Teilchen von einem Kamm zum nächsten oder von einem Tal zum nächsten wandert. Also sagen wir, es ist gefahren.
Das Pendel führt einen vollständigen Schwung aus, wenn es sich eine bestimmte Höhe von der Gleichgewichtsposition entfernt, den tiefsten Punkt passiert, auf der Hinfahrt auf die gleiche Höhe ansteigt und auf der Rückfahrt auf die Anfangshöhe zurückkehrt.
Zeitraum
Da sich die Wellen wiederholen, ist die Bewegung der Teilchen periodisch. Die Periode ist die Zeit, die benötigt wird, um eine vollständige Schwingung auszuführen, und wird normalerweise mit dem Großbuchstaben T bezeichnet. Die Einheiten der Periode im SI International System sind die Sekunden..
Frequenz
Sie ist die inverse oder reziproke Größe der Periode und hängt mit der Anzahl der pro Zeiteinheit ausgeführten Schwingungen oder Zyklen zusammen. Es ist mit dem Buchstaben gekennzeichnet F..
Da die Anzahl der Schwingungen keine Einheit ist, werden Sekunden für die Frequenz verwendet-1 (s-1), genannt Hertz oder Hertz und abgekürzt Hz.
Als Umkehrung der Periode können wir eine mathematische Beziehung zwischen beiden Größen schreiben:
f = 1 / T.
Ach ja:
T = 1 / f
Wenn beispielsweise ein Pendel 30 Zyklen in 6 Sekunden ausführt, ist seine Frequenz:
f = (30 Zyklen) / (6 s) = 5 Zyklen / s = 5 Hz.
Wellenlänge
Dies ist der Abstand zwischen zwei Punkten einer Welle, die sich auf derselben Höhe befinden, vorausgesetzt, eine vollständige Schwingung wurde durchgeführt. Sie kann beispielsweise von einem Kamm zum anderen in einer Reihe gemessen werden, aber auch von Tal zu Tal.
Die Wellenlänge wird mit dem griechischen Buchstaben λ bezeichnet, der als "Lambda" gelesen wird und in Entfernungseinheiten wie Metern im internationalen System gemessen wird, obwohl es eine so große Vielfalt von Wellenlängen gibt, dass Vielfache und Untermultiplikatoren häufig sind.
Wellenzahl
Es ist die inverse Größe der Wellenlänge, multipliziert mit der Zahl 2π. Wenn wir also die Wellenzahl mit dem Buchstaben k bezeichnen, haben wir:
k = 2π / λ
Ausbreitungsgeschwindigkeit
Es ist die Geschwindigkeit, mit der sich die Störung ausbreitet. Wenn das Medium, in dem sich die Welle ausbreitet, homogen und isotrop ist, dh seine Eigenschaften überall gleich sind, dann ist diese Geschwindigkeit konstant und ist gegeben durch:
v = λ / T.
Die Einheiten für die Ausbreitungsgeschwindigkeit sind die gleichen wie für jede andere Geschwindigkeit. Im internationalen System entspricht es m / s.
Da die Periode die Umkehrung der Frequenz ist, kann sie auch ausgedrückt werden:
v = λ. F.
Und da die Geschwindigkeit konstant ist, ist auch das Produkt λ.f konstant, so dass sich beispielsweise die Frequenz ändert, wenn beispielsweise die Wellenlänge geändert wird, so dass das Produkt gleich bleibt.
Verweise
- Giancoli, D. 2006. Physik: Prinzipien mit Anwendungen. 6 .. Ed Lehrlingshalle.
- Hewitt, Paul. 2012. Konzeptionelle Physik. 5 .. Ed. Pearson.
- Sears, Zemansky. 2016. Universitätsphysik mit moderner Physik. 14 .. Ed. Band 1. Pearson.
- Serway, R., Jewett, J. (2008). Physik für Wissenschaft und Technik. Band 1. 7 .. Ed. Lernen einbinden.
- Tipler, P. (2006) Physik für Wissenschaft und Technologie. 5. Aufl. Band 1. Editorial Reverté.



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.